planning
time elastic band
YeeKal
•
•
"#planning"
Elastic Band
EB is a local planner which needs an origin path to optimize.
two force:
- internal contraction force: 收缩力,消除松弛,张紧路线
- external repulsive force: 障碍物的排斥力
performance:
- handle dynamic obstacles
- may fail when changes are large(resort to global planner)
external potential energy
Bubbles
在b位置与障碍物的最小距离,这实际上定义了一个无障碍的圆空间:
则b处的bubble:
而elastic band可以看作是由有限个bubble组成。落在这些bubbles中的点保证是无碰撞的。为了保证路径无碰撞,假设各个相邻bubble重叠,则连接邻近bubble的圆心的线段可以保证无碰撞。
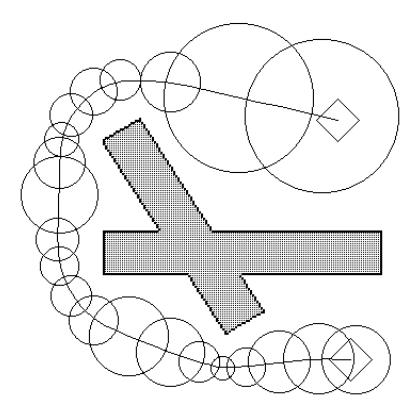
距离障碍物越近,bubble越小,数量也会越多。bubble的形状不限于圆形,也可以为椭圆,但是计算量会增大。
force demonstration
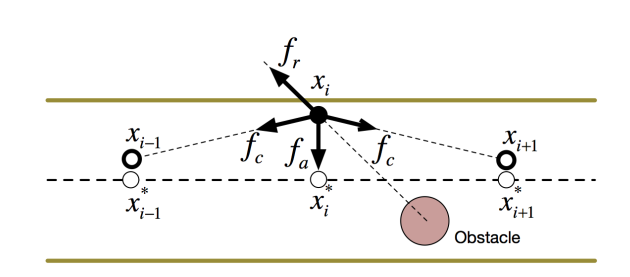
deform strategy
Time Elastic Band
global planner -> local planner
Teb 把各种约束条件通过线性相加的形式整合到一起(scalarized multi-objective optimization problem),比如时间/路径长度/避障/动力学约束/运动学约束/集合约束。这些约束大部分依赖于局部的运动状态,其结构可以使用稀疏矩阵来表述,因而可以方便地使用g2o优化库来解决。
optimization problem
TEB is a local planner
- configuration: $Q=\left{\mathbf{x}{i}\right}$} \quad n \in \mathbb{N
- time sequence: $\tau=\left{\Delta T_{i}\right}_{i=0 \ldots n-1}$
- TEB: $B:=(Q, \tau)$, a tuple of both sequence
运动被视为在teb上一系列的约束函数的集合,规划则是在约束的基础上找到最优的序列。这些约束一般是针对局部特性而言,因此约束的系数矩阵将会是一个对称的稀疏矩阵,这能够极大加速优化过程。
hyper-graph
把该稀疏系统以hyper-graph的形式表示
为了让边界约束可微,论文设计了一个函数:
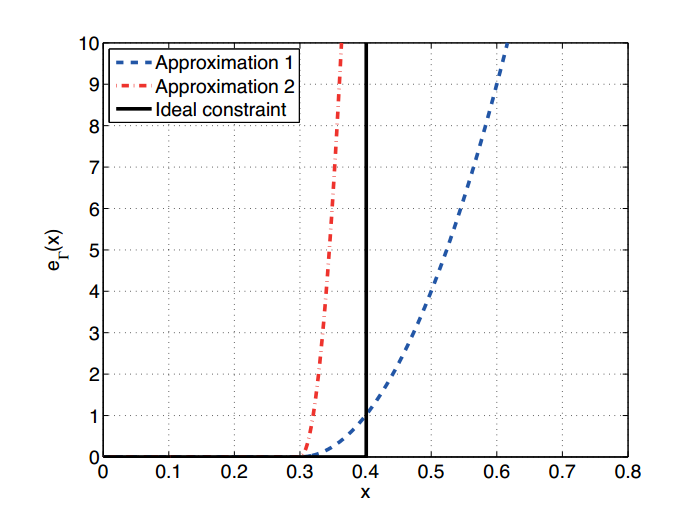
obstacles
velocity and acceleration
non-holonomic kinematics
fastest path
之前的elastic band通过“收缩力”减少路径长度,这里是定义了时间长度作为优化目标
ref
- blog
- projects
- paper
- elastic band
- common
- extensive
- 2015 Planning of Multiple Robot Trajectories in Distinctive Topologie -2017 Integrated online trajectory planning and optimization in distinctive topologies
- 2017- Kinodynamic Trajectory Optimization and Control for Car-Like Robots
- 2014 TEB + NMPC: Timed-Elastic-Bands for Predictive Control
- 2015 TEB + NMPC: Timed-elastic-bands for time-optimal point-to-point nonlinear model predictive control
- 2014-Planning of optimal collision avoidance trajectories with timed elastic bands
- 2015- A Convex Optimization Approach to Smooth trajectoriesfor Motion Planning with Car-Like Robots