34_optimal_control
Optimal Control :
- direct methods: transform into Nonlinear Program
- single shooting: discretized controls
- collocation: discretized controls and states
- multiple shooting: controls and node start values
- Indirect methods, Pontryagin: Solve Boundary Value Problem
-
Hamilton-Jacobi-BellmanEquation: Tabulation in State Space
-
locally optimal control
- shooting
- collocation
- forward dynamics models and shooting
- lqr
- ddp
ODE(Ordinary differential equation): 常微分方程
| Indirect method | Direct method | |
|---|---|---|
| Solution Scheme | First optimize, then discretize(e.g. Pontryagin (PMP)) | First discretize, then optimize (transfer the infinite problem into finite- imensional Nonlinear Programming problem (NLP), and solve NLP) |
| Pros | 1. Boundary value problem with only 2n_x ODE 2. can treat large scale systems | 1. can use state-of-the-art methods for NLP solution 2. can treat inequality constraints and multipoint constraints much easier |
| Cons | 1. only necessary conditions for local optimality2. Need explicit expression for control u*(t), singular arcs difficult to treat3. ODE is strongly nonlinear and unstable4. inequalities lead to ODE with state-dependent switches | 1. obtain only suboptimal/approximate solution |
| Applications | optimal control e.g. in satellite orbit planning at CNES | most commonly used nowadays due to their easy applicability and robustness |
optimal control problem in ODE
shooting
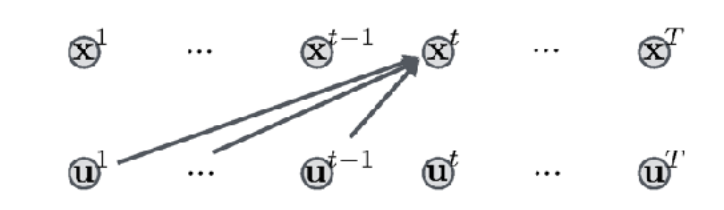
对定步长时间序列,通过选择基函数作为参数方程对控制变量参数化: $u(t,q)$
$x(t)$则被视为因变量,通过对状态方程积分得到。因此有可以被写为$x(t,q)$. 如此转化为关于q的最优化问题。根据积分后与最终目标的误差得到关于参数的梯度,从而通过不断调整参数改变控制量使得能射中目标。这里的参数方程可以是一个常数值,也可以是一条曲线。
shooting方法中的开环控制:
multiple shooting
- breaks down the system integration into short time intervals
- originally developed for PMP two-point BVPs
collocation
shooting方法是把控制量当作参数,根据动力学约束方程推导x,再根据目标函数求梯度。而collocation是随机初始化控制量和状态量,而把状态方程只是当作约束。
inverse dynamic function:
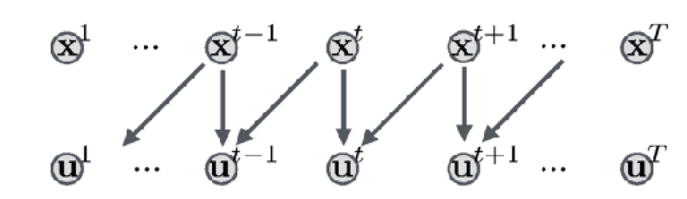
直接法的首要问题是如何解构动力学方程。最优化问题一般都是把变量离散化进行处理。如果把控制量当作优化变量,把状态变量当作临时变量,临时变量通过状态方程由控制变量得出,并只在乎最后状态是否达到了目标,则这就是shooting方法。如果把控制量和状态变量都当作优化变量,状态方程作为约束方程,则这就是collocation方法。一般,如果只把状态变量作为优化变量,控制量由逆状态方程得出,也被成为collocation方法。直接法的第二大问题就是如何离散状态方程,一般有牛顿积分法,荣格-库塔积分,辛普什积分等等。
最优控制的路径约束
numerical quadrature in collocation
Hermite-Simpson collocation method
基本形式:
应用到状态微分方程:
其中$f_{k+\frac{1}{2}}$是未知量,通过计算可得(ref):