st图
S-T graph
在既有路径的情况下进行速度规划,即确定当前的(路经点上的)最优速度。
以时间t为横轴, 路径长度为纵轴。图中的点表示在t时刻路径s的位置会与障碍物发生碰撞,因此可以根据该图进行最优速度的优化.
静态障碍物:
1. 根据路径序列计算碰撞的上下界
2. 在上下界加入时间上下界(时间起点和终点)形成四个点
3. 在st中的表现应该是横穿的矩形
动态障碍物:
1. 动态障碍物以离散轨迹点表示
2. 遍历轨迹点,对每个点在s路径序列上计算上下界,并加上当前时间
3. 把轨迹点的上界连起来,下界连接来,则在图中形成一个上下的包围体
在实际应用中有两大类不同的处理方案:
- time window(TW): 离散s轴,沿t轴方向画条带, 优化变量 $t_i$
- pass window(PW): 离散t轴,在s轴方向画条带, 优化变量为$s,\dot{s}, \ddot{s}$
PW 型
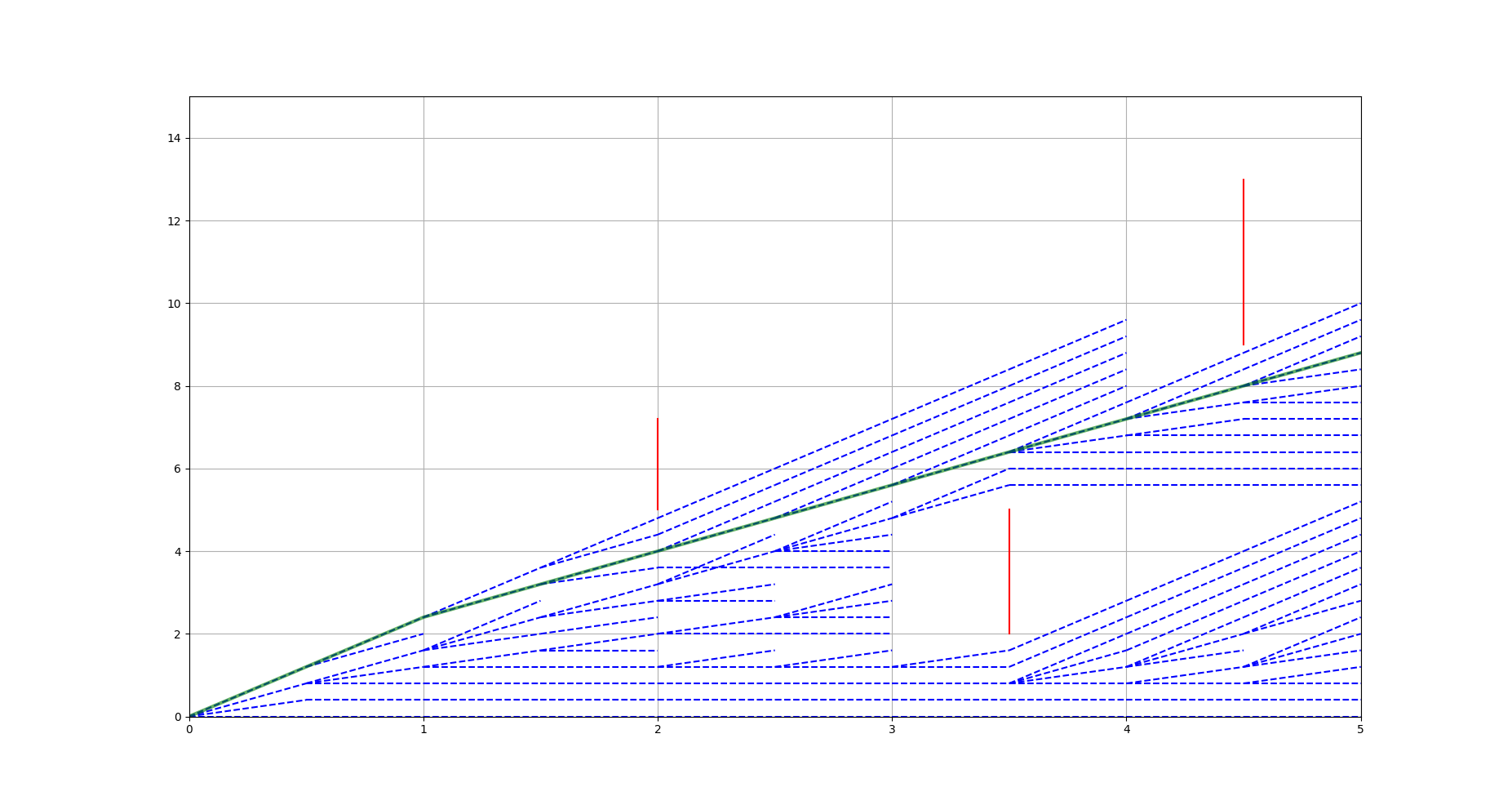
TW 型
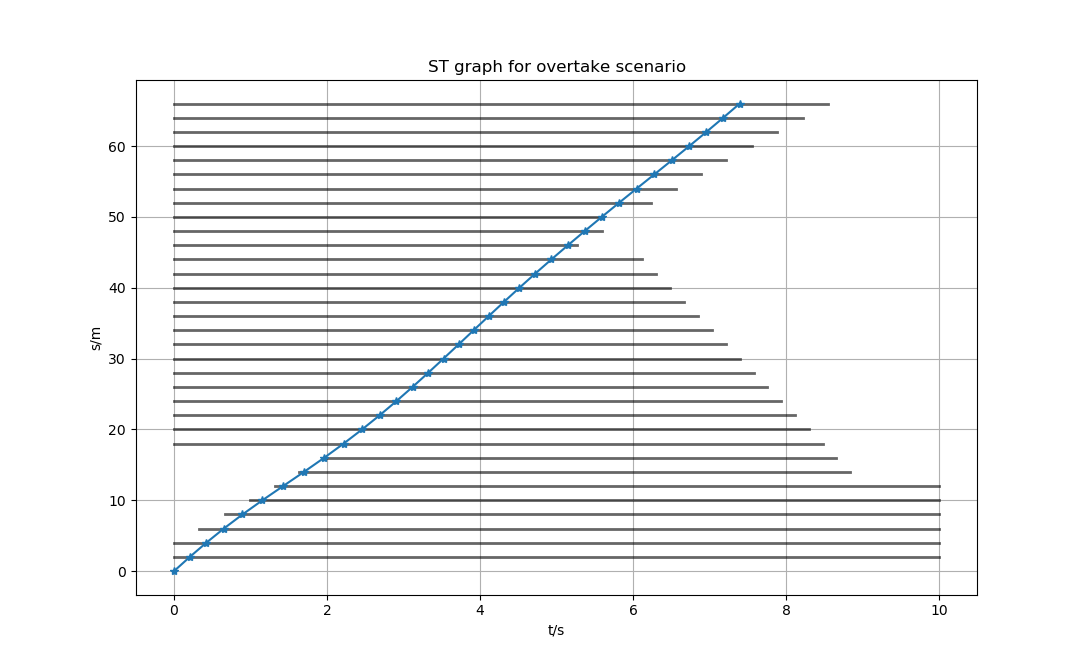
对于变量的处理上也有两大类:
- 直接离散变量
- 曲线拟合:多项式/贝塞尔曲线
PW 型
离散t轴,在s轴方向画条带, 优化变量为$s,v = \dot{s}, a = \ddot{s}, jerk$. 该问题可以转化为标准的QP问题,可以用OSQP进行快速求解。
问题定义只能在s方向上定义,不能对笛卡尔坐标系进行定义。因此关于曲率,横向加速度等没有办法加入到约束条件。
Cost function
Constraint
boundary constraint - safety
N = 4*t
s的约束规定了障碍物的时序
单调约束
N = t-1
状态方程约束/运动学约束 - kinematic
N = 3*(t-1)
scenario
纵向避让: 自车以当前速度行驶反应时间的距离后与前车应该保持安全距离
纵向超车: 自车以当前速度行驶反应时间内,被超车辆与自车能保持一定安全距离
PW 型 spline 参数曲线
s不再是离散变量,而是把s表示为t的曲线函数。早期Apollo的做法即是如此。在Apollo中,ST速度参数被分为 n 段,每段路径用用5阶多项式表示
如此优化变量从${s,v = \dot{s}, a = \ddot{s}, jerk}$转化为曲线的参数 ${a_{ij}}$,最后同样转化为QP问题
定义样条段优化函数
Apollo首先定义$cost_1$以使路径更加平滑:
然后,Apollo定义$cost_2$表示最后的S-T路径和S-T巡航路径(有速度限制且m个点)的差值:
同样地,Apollo定义了$cost_3$表示第一个S-T路径和随后的S-T路径(o个点)的差值:
最后得出的目标函数为:
约束条件
初始点约束
假设第一个点是($t0$, $s0$),且$s0$在路径$f_i(t)$, $f'i(t)$, 和$f_i(t)''$上(位置、速率、加速度)。Apollo将这些约束转换为QP约束的等式为:
单调约束
路线必须是单调的,比如车辆只能往前开。
在路径上采样 m 个点,对每一个 $j$和$j-1$ 的点对,且($j\in[1,...,m]$),如果两个点都处在同一个样条$k$上,则:
如两个点分别处在不同的样条$k$和$l$上,则:
平滑节点约束
该约束的目的是使样条的节点更加平滑。假设两个段$seg_k$ 和$seg_{k+1}$互相连接,且$seg_k$的累计值 s 为$s_k$。计算约束的等式为:
即:
然后,
等式中得出的结果为$t_0$ = 0。
同样地,为下述等式计算约束等式:
点采样边界约束
在路径上均匀的取样 m 个点,检查这些点上的障碍物边界。将这些约束转换为QP约束不等式,使用不等式:
首先基于道路宽度和周围的障碍物找到点 $(s_j, l_j)$的下边界$l_{lb,j}$,且$j\in[0, m]$。计算约束的不等式为:
同样地,对上边界$l_{ub,j}$,计算约束的不等式为:
速度边界优化
Apollo同样需要建立速度限制边界。
在st曲线上取样 m 个点,为每个点$j$获取速度限制的上边界和下边界,例如$v{ub,j}$ 和 $v{lb,j}$,约束定义为:
即:
且, 即:
TW型
优势:
- 沿路径限速:曲率限速,横向margin限速
- 横向加速度:
两大类优化方程结构:
- 以$t_i$为优化变量, 路径上的限速信息以及横向加速度转化为t的线性不等式 ref
- 以$v_i,a_i$为优化变量,路径上的限速信息直接使用$v_i$代替
优化变量$v(s), a(s)$
数据输入:
- $P={x_i,y_i,\theta_i}$
- $TW = {s_i,t_{min,i}, t_{max,i}}$
优化目标:
(优化目标暂时缺少横向运动学惩罚项,缺少加速度惩罚项)
约束方程:
Ref
ref: Apollo代码中的ST Graph在modules/planning/lattice/behavior/path_time_graph.h文件