ch2 feature detection

corner detector

• Shi-Tomasi corner detector
• Harris corner detector

Moravec detector

• 1977

Measure inetnsiry variation at $(x,y)$ by shifting a small window (3x3 or 5x5) by one pixel in each of the eight principle directions (horizontally, vertically, and four diagonals).

$$S_w(\Delta x,\Delta y)=\sum_{x_i\in w}\sum_{y_i\in w}(f(x_i,y_i)-f(x_i-\Delta x,y_i-\Delta y))^2 \\ \Delta x,\Delta y \in [-1,0,1],S_w(-1,-1),S_w(-1,0),\cdots$$

• not rotationally invariant as the intensity variation is only calculated at a discrete set of shifts

Harris corner detector

参考opencv

自相关函数(auto-correlation function)

$$E(u,v)=\sum_{x,y}w(x,y)[I(x+u,y+v)-I(x,y)]^2$$

• $w(x,y)$ is the window at position (x,y)
• $I(x,y)$ is the intensity at (x,y)
• $I(x+u,y+v)$ is the intensity at the moved window $(x+u,y+v)$
• uses a gaussian window instead of a square window

公式表示的含义是当图像沿着$(u,v)$方向移动时，图像在各个像素点的变化强度的总和。而角点应该是变化强度最大的地方。通过泰勒展开可以将上式变化为： $$M=\sum_{x,y}w(x,y)\begin{bmatrix} I_x^2 & I_xI_y \\I_xI_y & I_y^2\end{bmatrix} \\ E(u,v)\approx \begin{bmatrix} u & v\end{bmatrix}M\begin{bmatrix} u \\v\end{bmatrix}$$

其中M表征了各个像素点的变化强度的总和，其中的强度矩阵又叫做Harris矩阵，根据Harris矩阵特征值判断角点的响应值。

算法详细步骤:

• 第一步：计算图像X方向与Y方向的一阶高斯偏导数Ix与Iy
• 第二步：根据第一步结果得到Ix^2 , Iy^2与IxIy值
• 第三步：高斯模糊第二步三个值得到Sxx, Syy, Sxy
• 第四部：定义每个像素的Harris矩阵，计算出矩阵的两个特质值
• 第五步：计算出每个像素的R值
• 第六步：使用3X3或者5X5的窗口，实现非最大值压制
• 第七步：根据角点检测结果计算，最提取到的关键点以绿色标记，显示在原图上。

定义角点响应函数 $$R=\det M-k(\text{trace} M)^2 \\ \det M =\lambda_1 \lambda_2 \\ \text{trace} M=\lambda_1+\lambda_2\\ k=0.04-0.06$$

• R只与M的特征值有关
• 角点： R为大数值正数；表示$\lambda_1,\lambda_2$都较大，在两个方向上的移动都会产生较大变化
• 边缘： R为大数值负数; 表示$\lambda_1>>\lambda_2 \text{ or }\lambda_2>>\lambda_1$
• 平坦区： R为小数值

算法特点：

• 旋转不变性
• 几何尺度没有不变性

handle scale change

Harris Laplace detector

Hough transformation(HT)

霍夫变换于1962年由PaulHough首次提出，最初的Hough变换是设计用来检测直线和曲线，起初的方法要求知道物体边界线的解析方程，但不需要有关区域位置的先验知识。这种方法的一个突出优点是分割结果的Robustness,即对数据的不完全或噪声不是非常敏感。然而，要获得描述边界的解析表达常常是不可能的。　后于1972年由Richard Duda & Peter Hart推广使用，经典霍夫变换用来检测图像中的直线，后来霍夫变换扩展到任意形状物体的识别，多为圆和椭圆。霍夫变换运用两个坐标空间之间的变换将在一个空间中具有相同形状的曲线或直线映射到另一个坐标空间的一个点上形成峰值，从而把检测任意形状的问题转化为统计峰值问题。

直线

过某一点$(x_0,y_0)$的直线方程满足：$y_0=k\cdot x_0+b$, 或者$b=-x_0\cdot k+y_0$. 则若以$x_0,y_0$为已知量，则所有过该点的直线的参数$(k,b)$在$k-b$坐标系下是一条直线。则$k-b$坐标系下不同直线的交点意味着以该点为参数的直线方程经过不同的$(x,y)$.

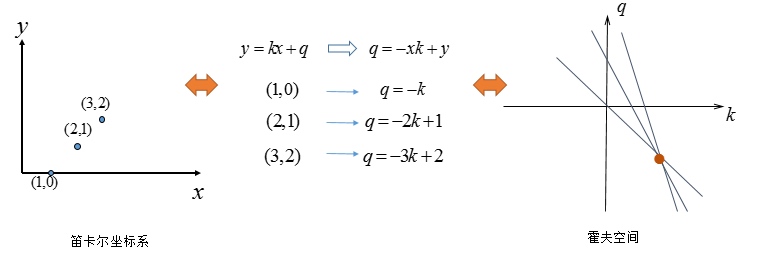
由于在实际中$k-b$坐标系无法表示$x=c$形式的直线，故实际中采用极坐标下的参数方程$d=x\cdot \cos(\theta)+y\cdot \sin(\theta)$, 参数空间为$(d,\theta)$.

推广

对于未知半径的圆，参数有三个，故参数空间是三维。而对于椭圆，参数空间升至5维。

广义霍夫变换(Generalized Hough Transform,GHT)

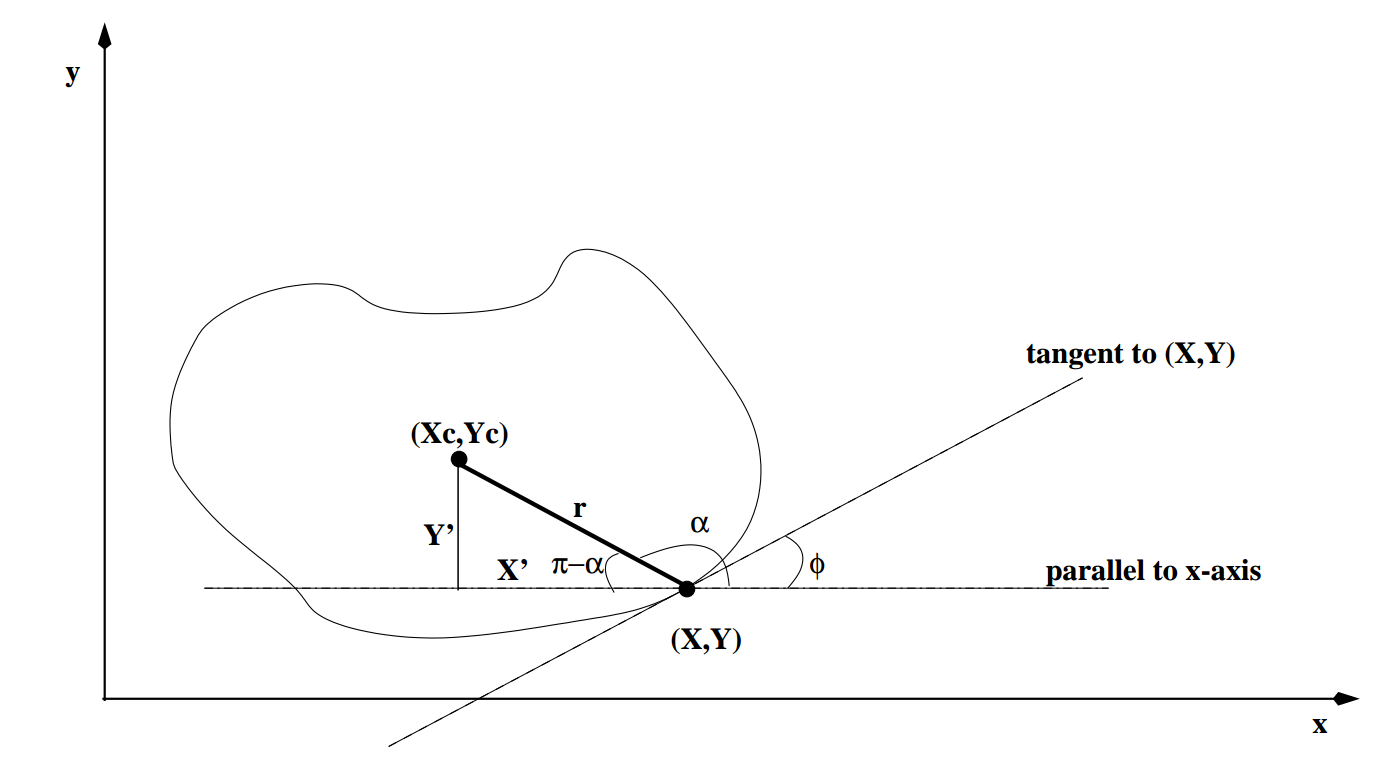
1. preprocessing

   • pick a reference point $(x_c,y_c)$
   • for each boundary point:
     • draw a line from reference point to this boundary point
     • compute $\phi$ (perpendicular to gradients's direction)
     • compute the distance $r$ and the feature angle $alpha$
     • store $(r,\alpha)$ as a function of $\phi$(R-table) $$\begin{align}\phi_1:&\quad (r_1^1,\alpha_1^1),(r_2^1,\alpha_2^1),\cdots \\ \phi_2:& \quad (r_1^2,\alpha_1^2),(r_2^2,\alpha_2^2),\cdots \\ \cdots \\ \phi_n:& \quad (r_1^n,\alpha_1^n),(r_2^n,\alpha_2^n),\cdots \end{align}$$

2. detection

   • quantize the parameter space:$P[x_{c_{min}},\cdots,x_{c_{max}}][y_{c_{min}},\cdots,y_{c_{max}}]$\
   • for each edge point $(x,y)$:
     • calculate $\phi$, and retrive from R-table all the $(r,\alpha)$ values indexed under $\phi$
     • for each $(r,\alpha)$, compute the candidate reference points: $$x_c=x+r\cdot \cos(\alpha)\\ y_c=y+r\cdot \sin (\alpha)$$
     • increase counters(voting):$++(P[x_c][y_c])$
   • if $P[x_c][y_c]>T$, then the object contour is located at $x_c,y_c$

3. detection(the object has undergone some rotation $\theta$ and uniform scaling $s$)

   • quantize the parameter space:$P[x_{c_{min}},\cdots,x_{c_{max}}][y_{c_{min}},\cdots,y_{c_{max}}][\theta_{min},\cdots,\theta_{max}][s_{min},\cdots,s_{max}]$
   • for each edge point $(x,y)$:
     • calculate $\phi$, and retrive from R-table all the $(r,\alpha)$ values indexed under $\phi$
     • for each $(r,\alpha)$, compute the candidate reference points: $$x'=r\cos(\alpha)\\ y'=r\sin(\alpha) \\ x_c=x+s_x\cdot(x' \cos(\theta)+y'\sin(\theta))\\ y_c=y+s_y \cdot(-x' \sin (\theta)+y'\cos(\theta))$$
     • increase counters(voting):$++(P[x_c][y_c])$
   • if $P[x_c][y_c][\theta][s]>T$, then the object contour is located at $x_c,y_c$, which has undergone a rotationn $\theta$, and has been scaled by s;
4. faster variations
   • hierarchical representation: First match using a coarse resolution Hough array, then selectively expand parts of the array having high matches
   • projections: Instead of having one high-dimensional array, store a few two dimensional projections with common coordinates ($e.g., (xc, yc), (yc,q), (q, s), (s, xc)$), then find consistent peaks in these lower dimensional arrays.