RANSAC
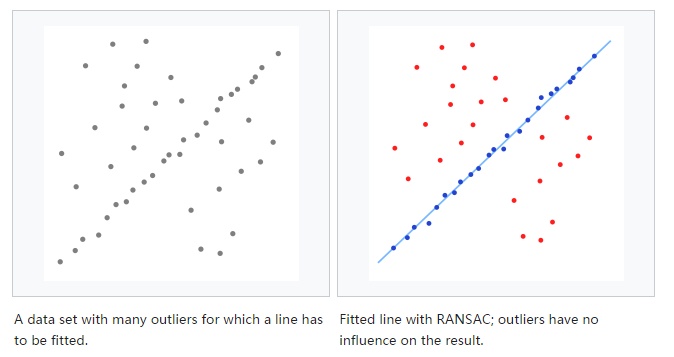
RANSAC (random sample consensus): 随机抽样一致算法。一种通过使用观测到的数据点来估计数学模型参数的迭代方法。比如对给定的一组数据来拟合直线,最小二乘法会拟合所有的点,而RANSAC会把点集分为inlier和outliner,只对inlier进行拟合。RANSAC首先随机采样n个样本,根据该样本估计模型,再根据模型查找总体样本中符合模型的样本数,通过不断迭代找到样本数最多(代价函数最小)的模型.
M. A. Fischler and R. C. Bolles (June 1981). "Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography". Comm. of the ACM 24: 381--395
Given:
data – a set of observed data points
model – a model that can be fitted to data points
n – minimum number of data points required to fit the model
k – maximum number of iterations allowed in the algorithm
t – threshold value to determine when a data point fits a model
d – number of close data points required to assert that a model fits well to data
Return:
bestfit – model parameters which best fit the data (or nul if no good model is found)
iterations = 0
bestfit = nul
besterr = something really large
while iterations < k {
maybeinliers = n randomly selected values from data
maybemodel = model parameters fitted to maybeinliers
alsoinliers = empty set
for every point in data not in maybeinliers {
if point fits maybemodel with an error smaller than t
add point to alsoinliers
}
if the number of elements in alsoinliers is > d {
% this implies that we may have found a good model
% now test how good it is
bettermodel = model parameters fitted to all points in maybeinliers and alsoinliers
thiserr = a measure of how well model fits these points
if thiserr < besterr {
bestfit = bettermodel
besterr = thiserr
}
}
increment iterations
}
return bestfit
how many samples(iterations) to choose
e = probability that a point is an outlier
s = number of points in a sample
N = number of samples (we want to compute this,iteration num)
p = desired probability that we get a good sample
Solve the following for N:
Choose N so that, with probability p, at least one random sample is free from outliers. e.g. p=0.99, solve N:
However, typically, we don't even have to sample N set. Early termination: terminate when inlier ratio reaches expected ration of inliers:
after RANSAC
RANSAC divides data into inliers and outliers and yields estimate computed from minimal set of inliers with greatest support. After that, improve this initial estimate with Least Squares estimation over all inliers (i.e., standard minimization).