YeeKal
c++

data type

YeeKal • •
"#c++"

哈希表

哈希表是一个[key-value]存储结构。通过哈希函数将键映射为索引值，从而达到时间复杂度为O(1)的查找速度。

哈希表是在时间和存储空间上作出权衡的一种结构。其查找速度快，但是占用内存多。

哈希函数：哈希函数应易于计算，且分布均匀。对于不同的的键类型(int,string)，需要不同的哈希函数。

一个计算string哈希值的函数。为了节省计算时间，采取每相隔8个字符去一次的方式计算。

public int GetHashCode(string str)
{
    char[] s = str.ToCharArray();
    int hash = 0;
    int skip = Math.Max(1, s.Length / 8);
    for (int i = 0; i < s.Length; i+=skip)
    {
        hash = s[i] + (31 * hash);
    }
    return hash;
}

哈希冲突

不同的键可能映射到同一个哈希值。

拉链法(Separate chaining with linked list): 每一个计算出的索引对应一个链表，按顺序存储相同哈希值的键所对应的值。

线性探测

树

  • 二叉查找树/二叉搜索树/二叉排序树：
    • 任意节点： left < middle < right
    • 没有键值相等的节点
    • 查找/删除/添加：$O(\lg n)$
  • 平衡二叉树(AVL)：二叉搜索树的一种。1. 可以是空树; 2. 若不为空，则左右子树都是平衡二叉树，即高度差不超过1. 保证了搜索时间在$O(\lg n)$

红黑树

红黑树，本质上来说就是一棵二叉查找树，但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡，从而保证了红黑树的查找、插入、删除的时间复杂度最坏为$O(\lg n)$. 红黑树通过对节点颜色的限制，保证了没有一条路径回避其他路径长处两倍，因此红黑树是一种弱平衡的二叉树，相对于要求严格的avl树，它的旋转次数少，所以对于搜索，插入，删除操作较多的情况下通常使用红黑树。

1. 每个节点要么是黑色，要么是红色。
2. 根节点是黑色。啊
3. 每个叶子节点（NIL）是黑色。
4. 每个红色结点的两个子结点一定都是黑色。
5. 任意一结点到每个叶子结点的路径都包含数量相同的黑结点。

优点： 红黑树不是高度平衡的，算是一种折中，插入最多两次旋转，删除最多三次旋转。

honghei1.png 红黑树的三种基本操作：左旋，右旋，变色

左旋

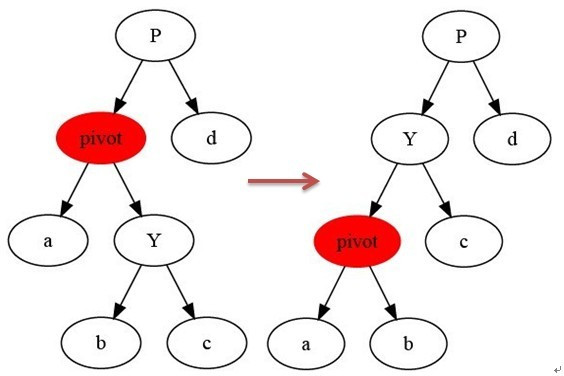
left_rotate.jpg

/* 
* 对红黑树的节点(x)进行左旋转
*
* 左旋示意图(对节点x进行左旋)：
*      px                              px
*     /                               /
*    x                               y                
*   /  \      --(左旋)-.           / \                #
*  lx   y                          x  ry     
*     /   \                       /  \
*    ly   ry                     lx  ly  
*
*
*/
    private void leftRotate(RBTNode<T> x){
        //设置x的右孩子为y
        RBTNode<T> y = x.right;

        //将 "y的左孩子" 设为 "x的右孩子"
        //如果y的左孩子非空，将 "x" 设为 "y的左孩子的父亲"
        x.right = y.left;
        if(y.left != null){
            y.left.parent = x;
        }

        //将 "x的父亲" 设为 "y的父亲"
        y.parent = x.parent;

        if(x.parent == null){
            this.mRoot = y;          //如果 "x的父亲" 是空结点，则将y设为根结点
        }else{
            if(x.parent.left == x){
                x.parent.left = y;   //如果 x是它父节点的左孩子，则将y设置为 "x的父节点的左孩子"
            }else{
                x.parent.right = y;  //如果 x是它父节点的右孩子，则将y设置为 "x的父节点的右孩子"
            }
        }

        // 将 “x” 设为 “y的左孩子”
        y.left = x;
        // 将 “x的父节点” 设为 “y”
        x.parent = y;
    }

右旋

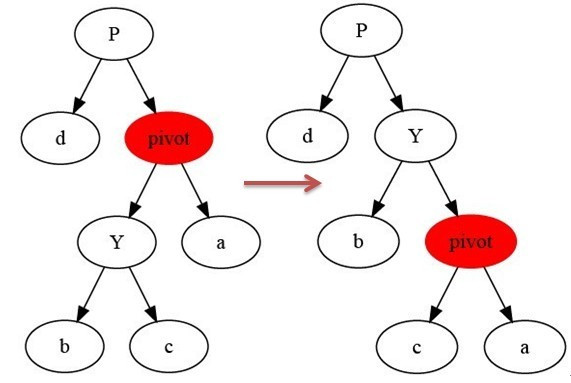
right_rotate.jpg

/* 
 * 对红黑树的节点(y)进行右旋转
 *
 * 右旋示意图(对节点y进行左旋)：
 *            py                               py
 *           /                                /
 *          y                                x                  
 *         /  \      --(右旋)-.            /  \                     #
 *        x   ry                           lx   y  
 *       / \                                   / \                   #
 *      lx  rx                                rx  ry
 * 
 */
private void rightRotate(RBTNode<T> y) {
    // 设置x是当前节点的左孩子。
    RBTNode<T> x = y.left;

    // 将 “x的右孩子” 设为 “y的左孩子”；
    // 如果"x的右孩子"不为空的话，将 “y” 设为 “x的右孩子的父亲”
    y.left = x.right;
    if (x.right != null)
        x.right.parent = y;

    // 将 “y的父亲” 设为 “x的父亲”
    x.parent = y.parent;

    if (y.parent == null) {
        this.mRoot = x;            // 如果 “y的父亲” 是空节点，则将x设为根节点
    } else {
        if (y == y.parent.right)
            y.parent.right = x;    // 如果 y是它父节点的右孩子，则将x设为“y的父节点的右孩子”
        else
            y.parent.left = x;    // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”
    }

    // 将 “y” 设为 “x的右孩子”
    x.right = y;

    // 将 “y的父节点” 设为 “x”
    y.parent = x;
}

插入

// step1: 按照二叉搜索树插入，并将插入节点涂为红色
// step2: 修复
//        |——若为根节点，直接涂为黑色
//        |——修复特性4
/*
 * 红黑树插入修正函数
 *
 * 在向红黑树中插入节点之后(失去平衡)，再调用该函数；
 * 目的是将它重新塑造成一颗红黑树。
 *
 * 参数说明：
 *     node 插入的结点        // 对应《算法导论》中的z
 */
private void insertFixUp(RBTNode<T> node) {
    RBTNode<T> parent, gparent;

    // 若“父节点存在，并且父节点的颜色是红色”
    while (((parent = parentOf(node))!=null) && isRed(parent)) {
        gparent = parentOf(parent);

        //若“父节点”是“祖父节点的左孩子”
        if (parent == gparent.left) {
            // Case 1条件：叔叔节点是红色
            RBTNode<T> uncle = gparent.right;
            if ((uncle!=null) && isRed(uncle)) {
                setBlack(uncle);
                setBlack(parent);
                setRed(gparent);
                node = gparent;
                continue;
            }

            // Case 2条件：叔叔是黑色，且当前节点是右孩子
            if (parent.right == node) {
                RBTNode<T> tmp;
                leftRotate(parent);
                tmp = parent;
                parent = node;
                node = tmp;
            }

            // Case 3条件：叔叔是黑色，且当前节点是左孩子。
            setBlack(parent);
            setRed(gparent);
            rightRotate(gparent);
        } else {    //若“z的父节点”是“z的祖父节点的右孩子”
            // Case 1条件：叔叔节点是红色
            RBTNode<T> uncle = gparent.left;
            if ((uncle!=null) && isRed(uncle)) {
                setBlack(uncle);
                setBlack(parent);
                setRed(gparent);
                node = gparent;
                continue;
            }

            // Case 2条件：叔叔是黑色，且当前节点是左孩子
            if (parent.left == node) {
                RBTNode<T> tmp;
                rightRotate(parent);
                tmp = parent;
                parent = node;
                node = tmp;
            }

            // Case 3条件：叔叔是黑色，且当前节点是右孩子。
            setBlack(parent);
            setRed(gparent);
            leftRotate(gparent);
        }
    }

    // 将根节点设为黑色
    setBlack(this.mRoot);
}

删除

1. 将红黑树当作一棵二叉查找树，将结点删除
2. 修正

哈夫曼编码

在解码中，出现频次最多的字母应该进行最少的字符占用，如此可降低编码所占用空间。所谓最少判断即是二叉树的带权路径最短。

前缀码：没有任何一个字符的编码是其他字符编码的前缀

  • 最优二叉树
  • 哈夫曼树

局限： 每个符号的编码长度只能为整数，所以如果源符号集的概率分布不是2负n次方的形式，则无法达到熵极限；输入符号数受限于可实现的码表尺寸；译码复杂；需要实现知道输入符号集的概率分布；没有错误保护功能

B 树

大规模数据存储中，二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁，进而导致查询效率低下

多叉树/平衡多路查找树

B树相对于平衡二叉树的不同是，每个节点包含的关键字增多了，特别是在B树应用到数据库中的时候，数据库充分利用了磁盘块的原理（磁盘数据存储是采用块的形式存储的，每个块的大小为4K，每次IO进行数据读取时，同一个磁盘块的数据可以一次性读取出来）把节点大小限制和充分使用在磁盘快大小范围；把树的节点关键字增多后树的层级比原来的二叉树少了，减少数据查找的次数和复杂度;

B+树

- 读写代价更低
- 查询效率更加稳定
← Back to cpp