loss function
-
regression loss function
-
classification loss function
introduction
关于损失函数(loss function),代价函数(cost function)和目标函数(Objective function)之间的区别和联系: - 损失函数 Loss Function 通常是针对单个训练样本而言,给定一个模型输出$\hat{y}$ 和一个真实$y$ ,损失函数输出一个实值损失$L=f(y_i,\hat{y_i})$ - 代价函数 Cost Function 通常是针对整个训练集(或者在使用 mini-batch gradient descent 时一个 mini-batch)的总损失 $J=\sum f(y_i,\hat{y_i})$ - 目标函数 Objective Function 是一个更通用的术语,表示任意希望被优化的函数,用于机器学习领域和非机器学习领域(比如运筹优化)
MSE
均方差损失(MSE, Mean Squared Error Loss)也称为L2 Loss. 基本形式:
在模型输出与真实值的误差服从高斯分布的假设下,最小化均方差损失函数与极大似然估计本质上是一致的,即均方差损失函数可以由最大似然估计推倒出来。因此在这个假设能被满足的场景中(比如回归),均方差损失是一个很好的损失函数选择;当这个假设没能被满足的场景中(比如分类),均方差损失不是一个好的选择。
MAE
平均绝对误差损失(MAE, Mean Absolute Error Loss)也称为L1 Loss. 基本形式:
假设模型预测与真实值之间的误差服从拉普拉斯分布(Laplace distribution)($\mu=0,b=1$),则给定一个$x_i$模型输出真实值$y_i$的概率为 与上面推导 MSE 时类似,我们可以得到的负对数似然实际上就是 MAE 损失的形式
MAE vs. MSE
- MSE 损失相比 MAE 通常可以更快地收敛
- MAE 损失对于 outlier 更加健壮,即更加不易受到 outlier 影响
Huber
取MSE和MAE各自的优点,也被称为Smooth Mean Absolute Error Loss.在误差接近 0 时使用 MSE,误差较大时使用 MAE.
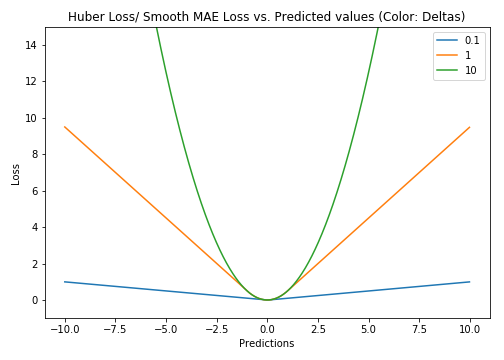
结合了 MSE 和 MAE 损失,在误差接近 0 时使用 MSE,使损失函数可导并且梯度更加稳定;在误差较大时使用 MAE 可以降低 outlier 的影响,使训练对 outlier 更加健壮。缺点是需要额外地设置一个 $\sigma$超参数
Quantile
分位数损失
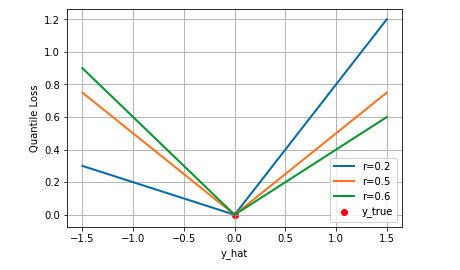
通常的回归算法是拟合目标值的期望或者中位数,而分位数回归可以通过给定不同的分位点,拟合目标值的不同分位数。当$r=0.5$时,分位数损失退化为 MAE 损失,从这里可以看出 MAE 损失实际上是分位数损失的一个特例 — 中位数回归.
Cross Entropy(交叉熵)
binary classification(二分类)
在二分类中我们通常使用 Sigmoid 函数将模型的输出压缩到 (0, 1) 区间内$\hat{y}_i\in (0,1)$ ,用来代表给定输入$x_i$后模型判断为正类的概率。在该类问题中通过最大似然估计得到交叉熵函数为:
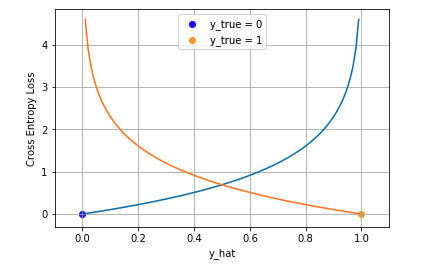 从图中可以看出越接近目标值损失越小。
从图中可以看出越接近目标值损失越小。
别名: Logistic Loss/Multinomial Logistic Loss
- Caffe: Multinomial Logistic Loss Layer. Is limited to multi-class classification (does not support multiple labels).
- Pytorch: BCELoss. Is limited to binary classification (between two classes).
- TensorFlow: log_loss.
多分类
在多分类的任务中,交叉熵损失函数的推导思路和二分类是一样的,变化的地方是真实值$y_i$现在是一个 One-hot 向量,同时模型输出的压缩由原来的 Sigmoid 函数换成 Softmax 函数。Softmax 函数将每个维度的输出范围都限定在(0,1)之间,同时所有维度的输出和为 1,用于表示一个概率分布。
则可以得到负对数似然函数为:
由于$y_i$是一个 one-hot 向量,除了目标类为 1 之外其他类别上的输出都为 0,因此上式也可以写为:
在多分类任务中,由于标签一般是one-hot向量,假设标签值为c,则简化为:
别名: Categorical Cross Entropy Loss.
- Caffe: SoftmaxWithLoss Layer. Is limited to multi-class classification.
- Pytorch: CrossEntropyLoss. Is limited to multi-class classification.
- TensorFlow: softmax_cross_entropy. Is limited to multi-class classification.
相对熵
也叫KL(Kullback–Leibler Divergence)散度,给定分布p,q,则两者的散度公式: 该公式衡量了两个分布之间的差异性,若p=q则散度为0.在分类问题中我们的目的是要学习到真实的分布,因此要最小化真实值和预测值分布的散度,而在散度公式中第一项完全由真实值分布确定,故优化目标函数变为$p\log{q}$,这与通过最大似然估计得到的交叉熵公式一致。
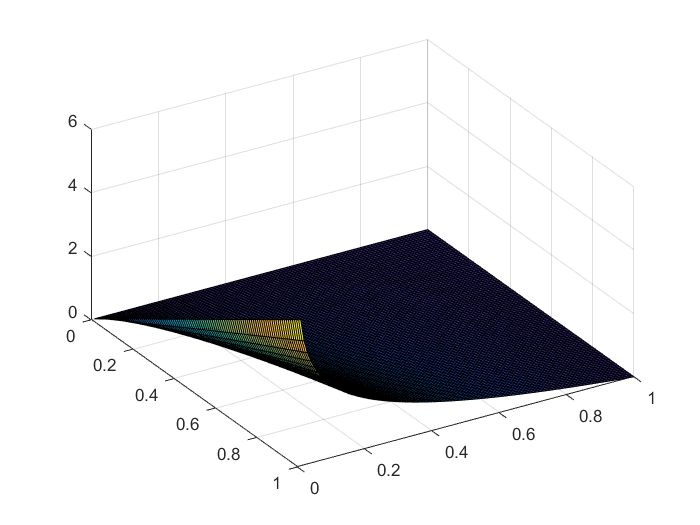
本质是用来衡量预测值$y_i$与真实值$y_i'$之间地距离。当然差地平方和也可以用来作为距离,但是交叉熵在某些问题上更有优势。从下图中的分布图可以看出,当真实值越大(接近于1)时,相同的误差$|y_i-\hat{y}_i|$产生的交叉熵越大,即在优化时所占比重越大。
%matlab
x=0:0.01:1;
y=0:0.01:1;
[xx,yy]=[xx,yy]=meshgrid(x,y);
zz1=-xx.*log(yy) %cross entropy
zz2=(xx-yy).^2 %
平方和:
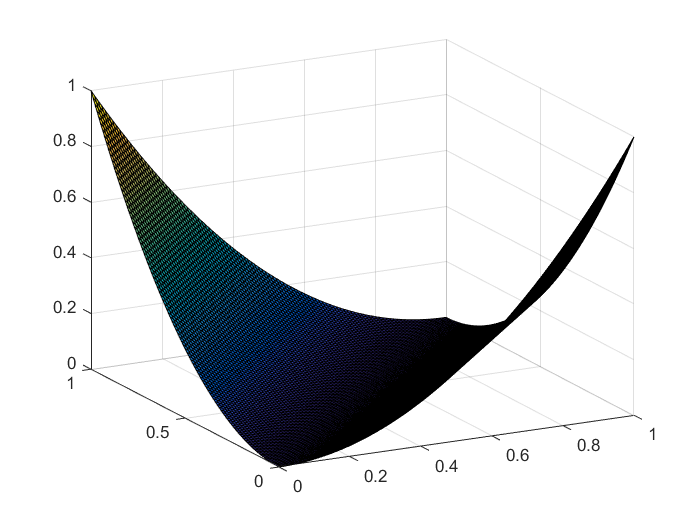
交叉熵:
Hinge Loss
合页损失
下图是$y$为正类, 即$sgn(y)=1$时,不同输出的合页损失示意图
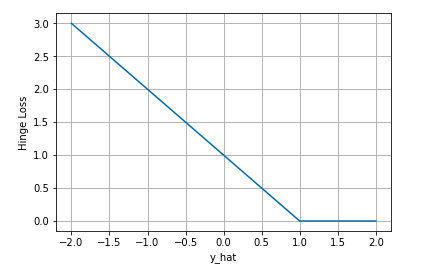
可以看到当$y$为正类时,模型输出负值会有较大的惩罚,当模型输出为正值且在(0,1)区间时还会有一个较小的惩罚。即合页损失不仅惩罚预测错的,并且对于预测对了但是置信度不高的也会给一个惩罚,只有置信度高的才会有零损失。使用合页损失直觉上理解是要找到一个决策边界,使得所有数据点被这个边界正确地、高置信地被分类。