决策树
Intro
决策树(decision tree)是组合判断条件进行决策的一类模型结构,当用于分类任务时又被称为分类树(classification decision tree);当用于回归任务时用被称为回归树(regression decision tree).但有时又统一用回归树来称呼两者。
决策树通过各个特征构建二叉树(多叉树),并将该树用于分类或回归任务。
- 节点(node)
- 内部节点(interior node): 分类节点,二叉树的除最低一层的节点
- 叶节点(leaf node): 结果节点,二叉树最低一层
- 有向边(directed edge)
- 分类树: 用于分类任务
- 回归树: 用于回归任务
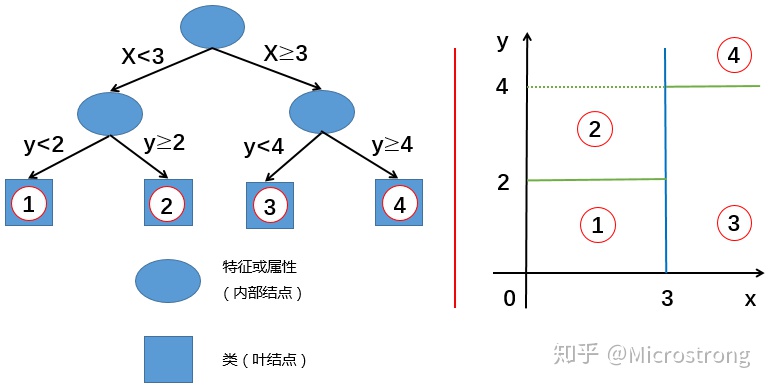
决策树的处理步骤一般分为三步:
- 选择一种构建算法,即以哪个目标来构建树
- 构建决策树
- 剪枝:优化树结构
特征选择策略
决策树的构建需要根据一种衡量指标(损失函数)来选择对哪个特征的哪个特征值进行分裂,这一过程又被称为特征选择(实际上是策略选择)或生成算法。实际上策略选择的过程就是损失函数选择的过程,在该损失函数的指标下,构建使得损失最小的一棵树。
树的生成算法:
|算法|支持模型 |树结构|特征选择|连续值|缺失值|剪枝|时间| |---|---|---|---|---|---|---|---|---| |ID3|分类 |多叉树|信息增益|不支持|不支持|不支持|1986| |C4.5|分类 |多叉树|信息增益率|支持|支持|支持|1993| |CART|分类/回归 |二叉树|基尼指数/均方差|支持|支持|支持|1984|
CART: 分类回归树(classification and regression tree), 既指树的生成算法,也有人把通过该算法生成的树叫做CART树.
信息熵(Information Entropy)
概率越小的事情信息量越大。一个事件的信息量随着发生的概率的减少而递减。信息熵代表了对该事件的信息量的期望。
条件熵
已知随机变量X的条件下随机变量Y的不确定性,$H(Y|X)$:
信息增益(Information Gain)
信息增益$g(D,A)$定义为集合$D$的信息熵与特征$A$在给定条件下$D$的条件熵$H(D|A)$之差(这又被称为互信息, mutual information):
- $|D|$: 样本容量
- $|C_k|$: 属于$C_k$类的个数
- $\sum_{k=1}^k|C_k|=|D|$: k个不同的取值分类的总个数为数据集的个数
- $\sum_{n=1}^n|D_k|=|D|$: 某一特征A有n个取值,根据n个取值把数据集划分为n份: $D_1, D_2, \cdots$
- $D_{ik}=D_i\cap C_k$: 子集$D_i$中属于类别$C_k$的集合
信息增益的计算:
- 计算数据集D的信息熵:
- 计算特征$A$在给定条件下$D$的条件熵$H(D|A)$:
- 计算信息增益:
信息熵表示了对数据集D分类的不确定性,而条件熵表示了按照特征A进行分类的不确定性,两者之差表示按照特征A进行分类该不确定性减少的程度。因此选择信息增益最大的特征表示有更强的分类能力。
信息增益率(Information Gain Ratio)
以信息增益作为划分存在偏向于选择取值较多的特征的问题,可以使用信息增益率对该问题进行矫正,即把该特征下的数据集的信息熵考虑进来:
基尼指数(Gini Index)
假设总共有k个分类,样本属于第$i$个分类的概率为$p_i$则概率分布的基尼系数:
样本集合D下的基尼系数
给定特征A下,集合D的基尼系数为:
过拟合
- 限制树的深度/尺寸
- [剪枝] 判断一棵子树存在分叉和没有分叉单独成为叶子节点时的误差,如果修剪之后误差更小,那么我们就减去这棵子树