凸集和凸函数
Linear Combination
线性组合 :
- 凸集(convex set): $\sum \lambda_i=1, \lambda_i \geq 0 $, $\rightarrow$Convex combination, Convex hull :
- 仿射集合(Affine set): $\sum \lambda_i=1$
- 凸锥(conic set): $\lambda_i \geq 0$ $\rightarrow$Conic combination, convec cone hull
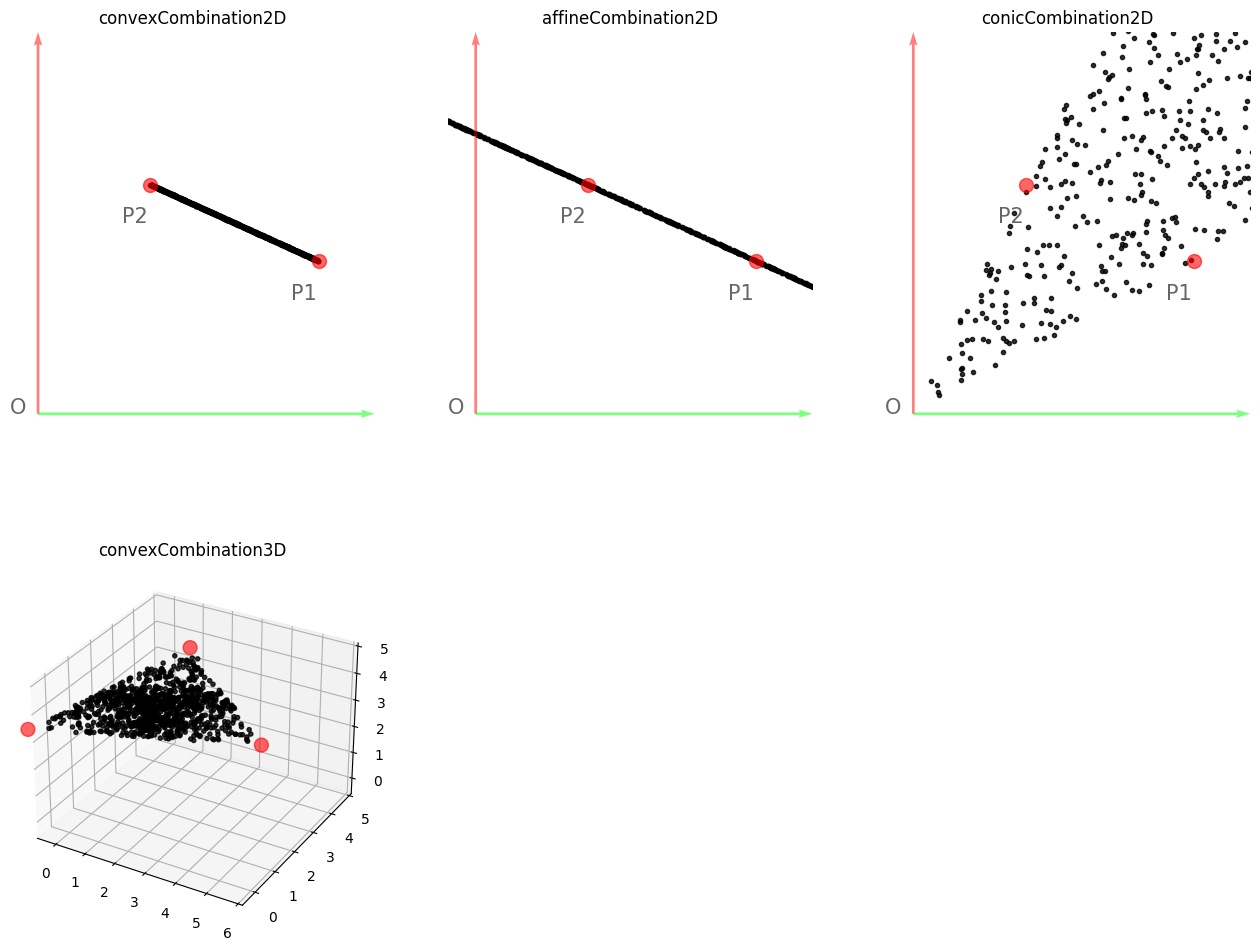
当选定了固定的$x_i$之后,通过凸线性组合则形成凸包(convex hull), 即包括这些点的最小凸集。通过凸锥组合则形成凸锥包(Convex cone hull), 即包括这些点的最小凸锥。
下图画出三种组合方式。可以看出,在2D情况下,凸组合是两点之前的线段;仿射组合是过两点的直线;而凸锥组合是原点分别向两个点连接的射线所包围的部分,类似一个尖锥。在3D情况下也可以看出,凸组合是包括了所有点的多面体,这也被称为 凸包(convex hull) .
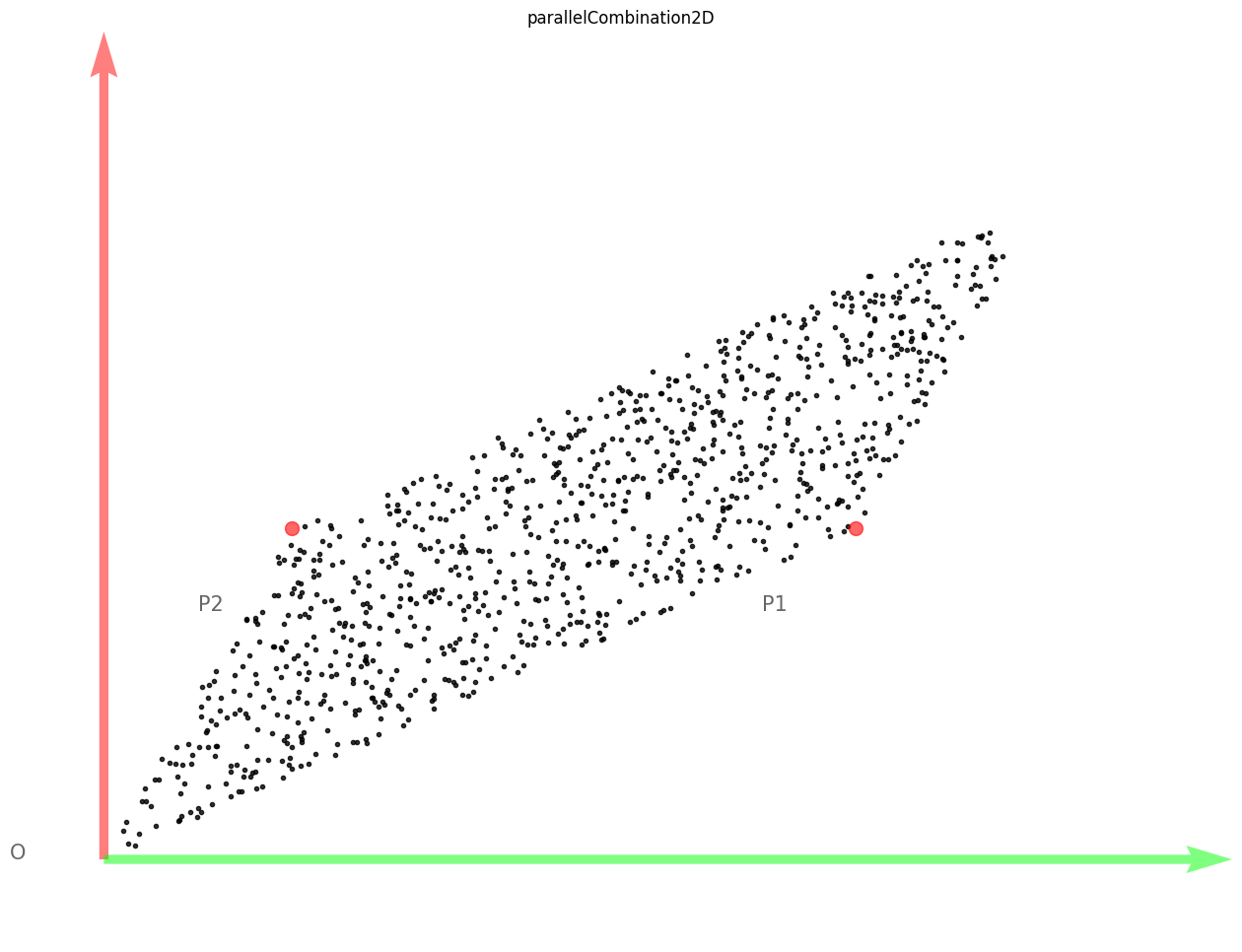
还有一些其他有意思的线性组合, 方形组合(我自己起得):
在二维平面, 对于两个向量, 方形组合 其实是以两个向量为边的平行四边行.
Convex Sets
Convex set:
$C \subseteq \mathbb{R}^n$ such that
In words, line segment joining any two elements lies entirely in set
Examples:
- 直线和线段:
- Norm ball: ${x: ||x||\leq r }$, for given norm $||\cdot||$, radius $r$
- Hyperplane: ${x: a^Tx = b}$
- Affine space: ${x: A^Tx = b}$
- Polyhedron(多面体): ${x: A^Tx \leq b}$
Affine Sets 仿射集
Affine Sets(仿射集): 通过两点的直线也在集合内
Convex Cones
Cone: $C\subset \mathbb{R}^n$ such that
对于一个向量空间$\mathrm{V}$与它的一个子集$\mathrm{C}$,如果子集$\mathrm{C}$中的任意一点x与 任意正数t, 其乘积at仍然属于子集$\mathrm{C}$, 则称$\mathrm{C}$为一个锥
给定任意点集,向外发散
Convex Cone: the conic combination of $x_1, \cdots, x_k\in \mathbb{R}^n$:
with $\theta_i \geq 0$
存在不是凸的锥。比如只有射线($y=|x|$),而没有内部. 而$y\geq |x|$是凸锥。
Examples of convex cones:
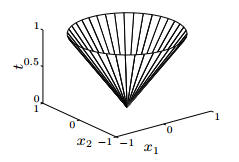
-Norm cone(标准锥): ${(x, t):||x|| \leq t }$, for a norm $||\cdot||$. Under $l_2$ norm $||\cdot||_2$, called second-order cone(二阶锥) -Normal cone - 对称半正定矩阵集合 $S^n_+$
下面也是一个二阶锥,只是对标准锥做了一个仿射变换:
几何视角
Hyperplane(超平面): ${x: a^Tx = b}$
a表示一个向量, b是一个标量, 整个表达式可以看为向量x在向量a的投影长度和向量a长度的乘积为b. a, b都是常量,因此x在a的投影长度也是一个定值, 所以可以想到x分布在一个与a垂直的平面上, 这个平面沿a方向远离原点的距离就是x在a的投影长度, 或者也可以说b定义了这个超平面的距离.
超平面是凸集、仿射集,只有在过原点的时候是个凸锥。
Affine space(仿射空间)
$L$ is an affine set $\iff L = {x|Ax = b}$ where $x \in R^n $, for some matrix $A$ and $b$.
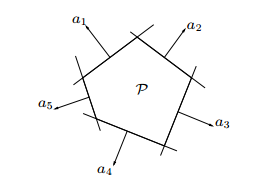
单纯性是线性组合的角度,而多面体是 多个线性不等式
多面体的定义: 线性不等式 + 等式约束
直线和线段
记$x_1,x_2\in C$,则直线形式:
若$\theta \in [0,1]$则y构成了$x_1$和$x_2$之间的线段。上述直线形式表示了y是基于两个基点所构成的,当$\theta \in [0,1]$y在两点之间变动;当$\theta <0$或$\theta > 1$,y则超出线段,在线段的延伸处。
Ball(球):
ball with center $x_c$ and radius r:
Ellipsoid:(椭圆):
or:
Norm ball / Norm cone:把二范数扩展到范数
norm ball: $||x-x_c|| \leq r$
norm cone: $||x|| \leq t$. euclidean norm cone is called second-order cone(二阶锥).
Polyhedra(多面体)
solution set of finitely many linear inequalities and equalities
Positive semidefinite cone(半正定锥)
$$$$
半正定矩阵$S^n_{+}$组成的集合是一个凸锥。
对称矩阵$S^n$组成的集合是一个凸锥。
线性组合 :
- 仿射集合(Affine set): $\sum \lambda_i=1$
- 凸锥(conic set): $\lambda_i \geq 0$
- 凸集(convex set): $\sum \lambda_i=1, \lambda_i \geq 0 $, $\rightarrow$Convex combination
一条线也是一个仿射集:$x=\theta x_1 +(1-\theta) x_2$.
线性方程组的解集$C={ x| Ax=b }$是一个仿射集合。反之,任意仿射集合可以表示为一个线性方程组的解集。上式中$A$是一个矩阵,$x,b$都是向量。
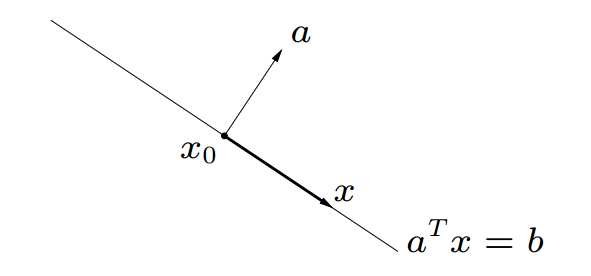
${ x| a^Tx=b }$这个集合被称为超平面,a,x是向量b是一个常数。任取$x_0$,使得$a^Tx_0=b$, 则解集上任意点$x$,有$a^T(x-x_0)=0$. 即解集以$x_0$为中心,垂直a的所有的线段形成的平面。或者可以理解为x在a上投影的长度为b,则满足条件的x在垂直于a的某一个平面上,而b决定了这个平面的高度。
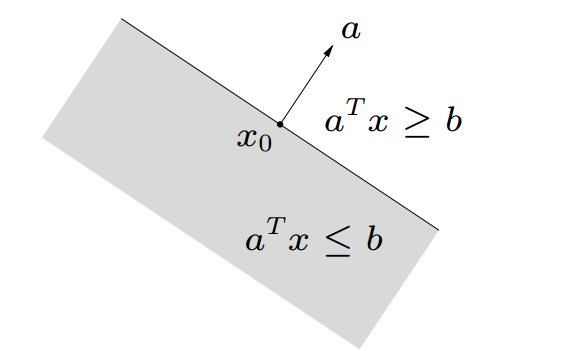 ${a^Tx \leq b }$ 被成为半空间(halfspace).可以认为是由超平面分割的空间。
${a^Tx \leq b }$ 被成为半空间(halfspace).可以认为是由超平面分割的空间。
超平面是仿射集,也是凸集,半空间是凸集。
上述图形表示,由$OP_1$和$OP_2$形成的锥体就是向量的凸锥,而线段$l1$是仿射集合,两者的交集,即线段$P_1P_2$是凸集。
从集合的角度理解一下优化问题:
- P是A的列向量组成的超平面相交之后再与凸锥($x\geq 0$)相交的集合
- $\mathbf{A} \mathbf{x}=\mathbf{b}, \mathbf{x} \geq \mathbf{0}$意味着,向量b落入由A的列向量形成的凸锥中。
Key properties of convex sets
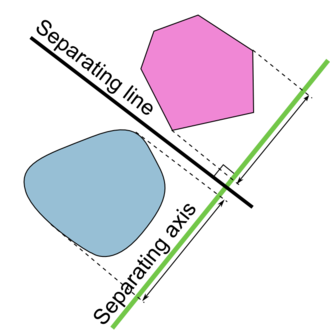
Separating hyperplane theorem(超平面分离定理) :
if $C$ and $D$ are nonempty disjoint convex sets, there exist $a \neq 0, b$ s.t.
the hyperplane $\left{x \mid a^{T} x=b\right}$ separates $C$ and $D$ strict separation requires additional assumptions (e.g., $C$ is closed, $D$ is a singleton)
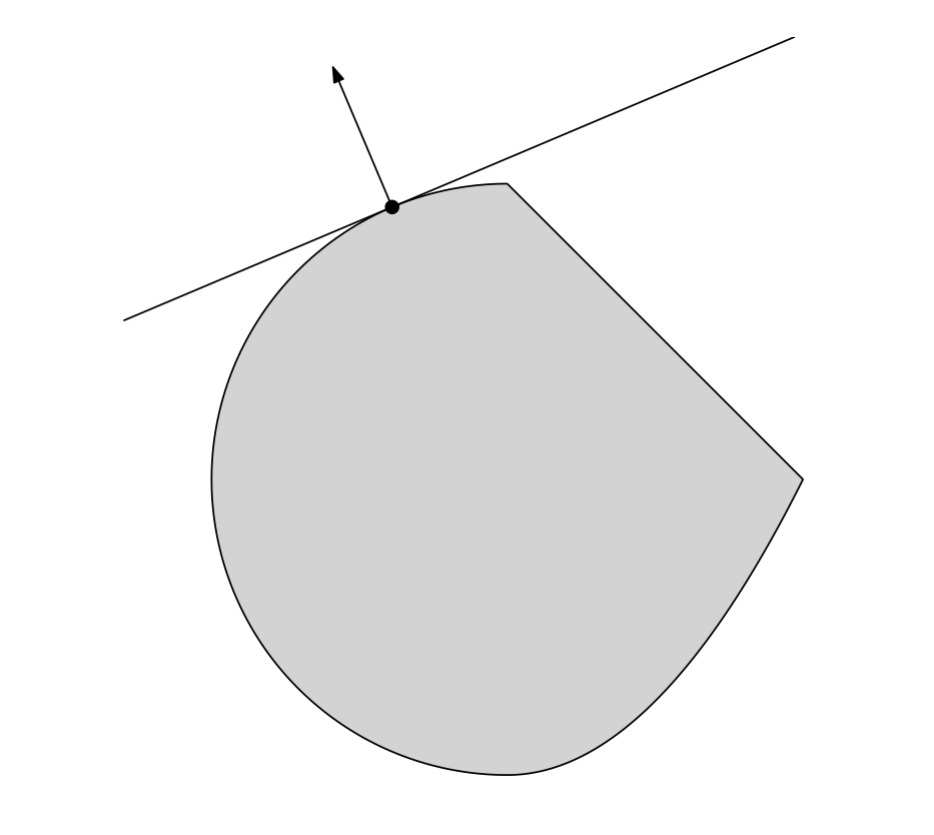
Supporting hyperplane theorem(超平面支持定理) :a boundary point of a convex set has a supporting hyperplane passing through it. Formally: if $C$ is a nonempty convex set, and $x_0\in bd(C)$, then there exists $a$ such that:
Operations that preserve convexity(保凸运算)
operations between convex set:
- intersection
- scaling and translation:
$C$ is convex $\rightarrow$ ${ ax+b : x\in C}$ is convex
- affine functions: affine images and preimages
If $f(x) = Ax+b$, then:
is convex. If $D$ is convex then: is convex.
- perspective function
- linear-fractional function
vintersection** : $S=\left{x \in \mathbf{R}^{m}|| p(t) \mid \leq 1 \text { for }|t| \leq \pi / 3\right}$
affine function
凸集经过仿射函数变换和逆变换都是凸的。
- scaling
- translation
- projection
perspective function(透视函数) $P: \mathbf{R}^{n+1} \rightarrow \mathbf{R}^{n}$ :
images and inverse images of convex sets under perspective are convex
linear-fractional function $f: \mathbf{R}^{n} \rightarrow \mathbf{R}^{m}$ : images and inverse images of convex sets under linear-fractional functions are convex
generalized inequalities (广义不等式)
a convex cone $K \subseteq R^n$ is a proper cone(正常锥) if:
- K is closed(contain its boundary)
- K is solid (has nonempty interior)
- K is pointed(contains no line)
examples
- 非负象限
- 半正定矩阵 $S^n_{+}$
- $[0,1]$上非负的多项式
由正常锥$K$定义的广义不等式:
通过减法操作后其结果属于对应的正常锥。
- element-wise 不等式: $x \preceq_{\mathbf{R}{+}^{n}} y \Longleftrightarrow x, \quad i=1, \ldots, n$} \leq y_{i
- matrix inequality: $X \preceq \mathbf{S}_{+}^{n} Y \quad \Longleftrightarrow \quad Y-X \text { positive semidefinite }$
a positive definite matrix A defines a sllipsoid:
the correspondence between $A$ and $\mathcal{E}_A$ is one-to-one, moreover, $A\succeq B$ if and only if $\mathcal{E}_B$ contains $\mathcal{E}_B$.
minimum and minimal elements
如果对于每个y, x都广义小于等于y,则x是集合的最小元(minimum element)。
如果若y广义小于等于x都能推出x与y相等, 则x是极小元(minimal element)。(类似极值点)
$x \in S$ is the minimum element of $S$ with respect to $\preceq_{K}$ if $x \in S$ is a minimal element of $S$ with respect to $\preceq_{K}$ if
凸函数
定义:
性质: - 凹函数 concave function: $f$ is concave if −$f$ is convex - 严格凸函数(Strictly Convex Function): 去掉不等式的等号.$f$ is strictly convex if dom $f$ is convex and $f(\theta x+(1-\theta) y) < \theta f(x)+(1-\theta) f(y), \quad 0< \theta < 1$ - 广义凸函数(Generalized Convex Function): 不要求函数可导 - 强凸函数(Strong convex):with parameter $m > 0: f-\frac{m}{2}||x||^2_2$ is convex. In words, $f$ is at least as convex as a quadratic function.
- $f$ is concave if −$f$ is convex
上镜图 (Epigraph/Supergraph): 在函数$y=f(⋅)$曲线及其上方的所有的点构成的集合:
当这个点集是凸集(Convex Set)的时候,对应的函数是凸函数,反之亦然
Examples:
- $e^{ax}$, for any $a$
- $x^{a}$, for any $a \geq 0$ or $a \leq 0$, is convex; $x^a$ is concave for $0\leq a \leq 1$
- $\log x$ is concave
- Affine function: $a^Tx+b$ is both convex and concave
- Quadratic function: $\frac{1}{2}x^TQx+b^Tx+c$ is convex provided that $Q \succeq 0$(positive semidefinite)
- Least square loss: $||y-Ax||^2_2$ is always convex, since $A^A$ is always positive semidefinite
- Norm: ||x|| is convex for any norm:
approve:Why is every p-norm convex?
一阶条件: 切线总是在函数的下方
First-order characterization
if $f$ is differentiable, then $f$ is convex if and only if dom($f$) is convex, and:
for all $x,y\in dom(f)$
一阶条件: 切线总是在函数的下方
Proof:
After rewriting, we have As $\lambda \downarrow 0$, we get
Second-order characterization
if $f$ is twice differentiable, then $f$ is convex if and only if dom($f$) is convex, and $\nabla^2f(x)\succeq 0 $ for all $x\in dom(f)$
Jensen's inequality: $f$ is convex, $X$ is a random variable supported on dom($f$), then:
Operations preserving convexity
Nonnegative linear combination:: $f_1, \cdots, f_m$ convex implies $a_1f_1+\cdots + a_mf_m$ convex for any $a_1, \cdots, a_m \geq 0$
Pointwise maximation:
Partial minimization:
Affine composition: $f$ convex implies $g(x) = f(Ax + b)$ convex
General composition:
Vector composition:
Example:
log-sum-exp function:
$g(x) = \log(\sum^k_{i=1} e^{a_i^Tx+b_i})$, often called softmax function, as it smoothly approximates $\max_{i=1,\cdots,k}(a_i^Tx+b_i)$
- First, note it suffices to prove convexity of $f(x)=\log \left(\sum_{i=1}^n e^{x_i}\right)$ (affine composition rule)
- Now use second-order characterization. Calculate
- Write $\nabla^2 f(x)=\operatorname{diag}(z)-z z^T$, where $z_i=e^{x_i} /\left(\sum_{\ell=1}^n e^{x_{\ell}}\right)$. This matrix is diagonally dominant, hence positive semidefinite
ref
- blog
- course
- books