12_gradient_decent
梯度下降步长的选择至关重要,不能太大或者太小。line search是线性搜索步长的一大类方法的统称。
Backtracking line search:
Backtrack: 回溯
要求: 目标函数要求可微并显式知道梯度函数
- select parameters $0<\beta < 1$ and $0< \alpha \leq 1/2$
- at each iteration, start with $t=1$, and while:
shrink $t = \beta t$, Else perform gradient descent update:
解释:对于当前点$x_i$,不同的$t$会产生不同的$f(x_i-t\nabla f(x_i))$,$f(x_i-t\nabla f(x_i))$在局部情况下会按照所期望的慢慢减小,但是如果$t$过大$f(x_i-t\nabla f(x_i))$不会减小很多,甚至会上升.知觉告诉我们在大部分情况下 $f(x_i-t\nabla f(x_i))$ 会是如下图实线所表示的一样是先下降后上升的趋势。为了近可能的降低$f$,希望当减小的较小的时候能或者是当步长越过最低值之后能减小$t$以减小步长。该方法的做法是对当前的切线 $f(x) - t||\nabla f(x)||^2_2$,标记为$l_1$放宽到$\alpha$倍,即$f(x) - \alpha t||\nabla f(x)||^2_2$,标记为$l_2$.$\alpha \in(0, 0.5)$,因此放宽之后的线会更加平缓。该方法对迭代步长之后的值进行了一下比较,如果迭代之后仍然在$l_2$上方,说明迭代的步长可能过长(?),以至于迈过了最优值,需要减小步长。
疑问点: 如果迭代之后仍然在$l_2$上方,也有可能是步长太短了,怎么能保证有效性?
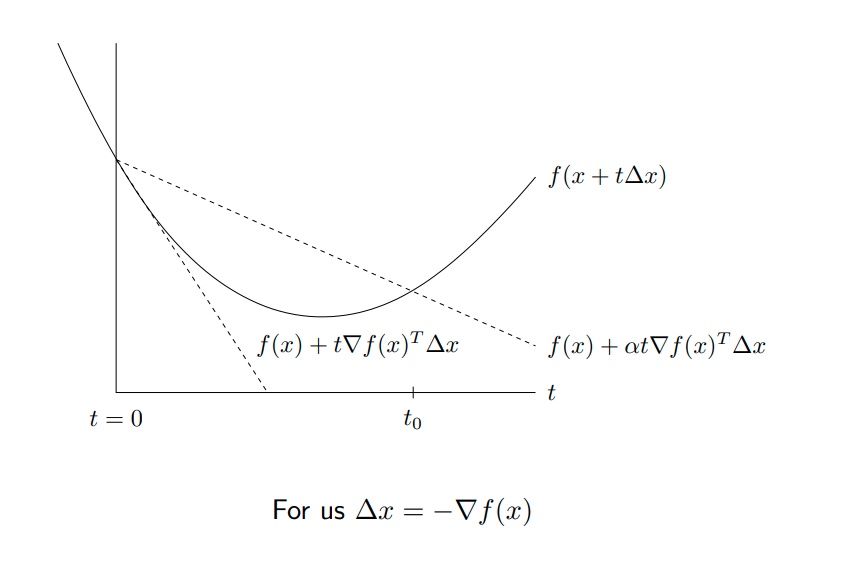
Armijo–Goldstein condition
校验以一定步长更新以后函数值是否能有效地收敛,防止较大的步长收敛速度较慢。如下图所示,l1是沿当前梯度的更新变化趋势, 是f的一个近似,步长约大约不准确。更新的原则希望f能够下降的较快,因此以l2做限制。由于$\alpha \in (0, 1/2)$, l2总是在l1上方。因此若f在l2上方,则说明f的下降趋势较慢,步长太大了需要缩小使得f落入l2一下。
- $\alpha \in (0, 1/2)$
- $d_k$: raw step
- $t d_k$: real step
Wolfe-Powell condition
使得更新点处的斜率减小
exact line search
choose step to do the best we can along direction of negative gradient.
Usually not possible to do this minimization exactly.
Convergence analysis
Assume that $f$ convex and differential, with $dom(f) = \mathbb{R}^n$, and additionally
I.e, $\nabla f$ is Lipschitz continuous with constant $L>0$.
Convergence analysis for gradient descent
Theorem: Gradient descent with fixed step size $t\leq 1/L$ satisfies:
We say gradient descent has convergence rate $O(1/k)$,i.e to get $f(x^k) - f^* \leq \epsilon$, we need $O(1/\epsilon)$ iterations
Proof:
- $\nabla f$ Lipschitz with constant $L \Rightarrow$
- Plugging in $y=x^{+}=x-t \nabla f(x)$,
- Taking $0<t \leq 1 / L$, and using convexity of $f$,
- Summing over iterations:
- Since $f\left(x^{(k)}\right)$ is nonincreasing,
Convergence analysis for backtracking
Theorem: Gradient descent with backtracking line search satisfies:
where $t_{min} = \min {1,\beta/L}$
if $\beta$ is not too small, then we dont lose much compared to fixed step size $(\beta/L \quad \text{vs}\quad 1/L)$
Convergence analysis under strong convexity
strong convexity: $f-\frac{m}{2}||x||^2_2$ is convex for some $m>0$. If $f$ is twice differentiable , then this implies
Sharper lower bound than that from usual convexity:
Theorem: Gradient descent with fixed step size $t\leq 2/(m+L)$ satisfies:
- rate with strong convexity is $O(c^k)$, exponentially fast
- to get $f(x^k) - f^* \leq \epsilon$, we need $O(1/\epsilon)$ iterations
Practice at the condition
A look at the conditions for a simple problem,$f(\beta) = \frac{1}{2}||y-X\beta||_2^2$
Lipschitz continuity of $\nabla f$: - This means $\nabla^2f(x)\preceq LI$ - As $\nabla^2f(\beta) = X^TX$, we have $L = \sigma^2_{max}(X)$
Strong convexity of $f$ : - This means $\nabla^2 f(x) \succeq m I$ - As $\nabla^2 f(\beta)=X^T X$, we have $m=\sigma_{\min }^2(X)$ - If $X$ is wide-i.e., $X$ is $n \times p$ with $p>n$-then $\sigma_{\min }(X)=0$, and $f$ can't be strongly convex - Even if $\sigma_{\min }(X)>0$, can have a very large condition number $L / m=\sigma_{\max }(X) / \sigma_{\min }(X)$
A function $f$ having Lipschitz gradient and being strongly convex satisfies: for constants $L>m>0$ Think of $f$ being sandwiched between two quadratics May seem like a strong condition to hold globally (for all $x \in \mathbb{R}^n$ ). But a careful look at the proofs shows that we only need Lipschitz gradients/strong convexity over the sublevel set This is less restrictive.
Practicalities
Stopping rules:
stop when $||\nabla f(x)||_2$ is small
- recall $\nabla f(x^) = 0$ at solution $x^$
- if $f$ is strongly convex with parameter $m$, then:
Forward stagewise regression
Steepest descent
Gradient boosting
不是更新函数的参数而是更新函数本身。如果有误差则添加一个新的函数
