optimization
barrier function
YeeKal
•
•
"#optimization"
把约束条件转化为目标函数的一部分,而约束条件转化为参数的范围约束。这些参数使得修改过的最优化问题的最优解在原始问题最优解的附近。对于一个特定的参数,可以很容易求出最优解。然后通过调整参数,使得最优解逼近原始问题的最优解。这种求解一系列无约束最优化的方法也被称为序列无约束极小化方法(SUMT: Sequential Unconstrained Minimization Technique)
Log Barrier Function
对于凸优化问题
可以增加log barrier函数,把优化目标改为:
其中约束条件$h_i(x) \leq 0$就是log函数的定义域,同时当$h_i(x)\rightarrow 0$时,log barrier会趋近于无穷大。因此若优化目标有最小值,则约束条件必能满足。其中$t>0$是一个很大的参数,用来调整log barrier函数对原优化目标的影响。
在每次求解的时候,固定参数t,求出当前的最优解。然后逐渐增大t,逼近原始问题的最优解。
其中barrier function 被定义为:
相关梯度和Hessian函数:
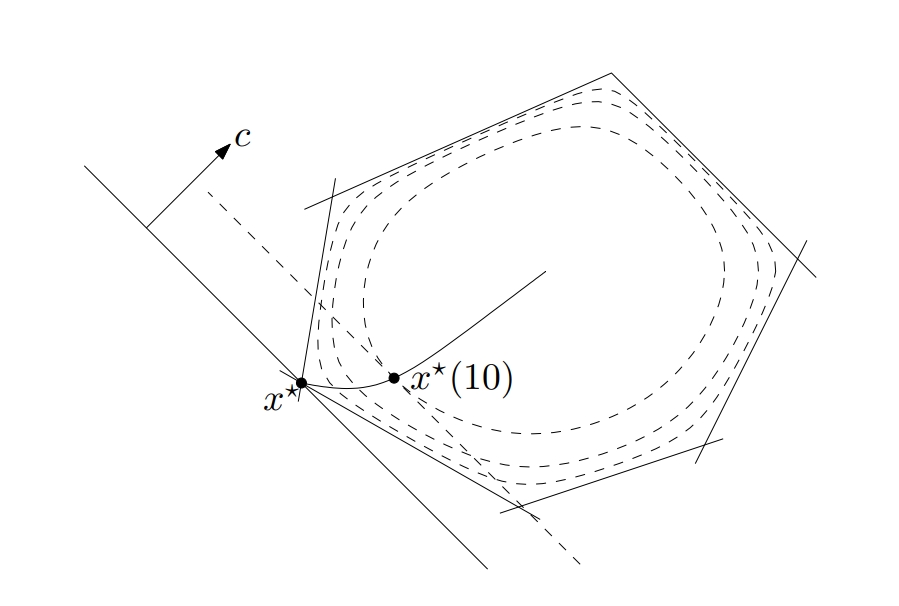
Central Path
根据log barrier函数重写优化目标:
central path被定义为最优解关于参数t的函数$x^*(t)$. 根据KKT条件:
对于线性优化,$f(x)=c^Tx$, 其central path $x^*(t)$如下图所示:
Ref
- course/slides
- blog