recsys
基于矩阵分解的协同过滤
YeeKal
•
•
"#recsys"
- topn 推荐: 准确率 / 召回率
- LFM(latent factor model): 隐因子模型,基于矩阵分解
- als/slope one
svd 分解
把打分矩阵当作一个大矩阵,并进行SVD分解,但是只保留部分奇异值进行预测:
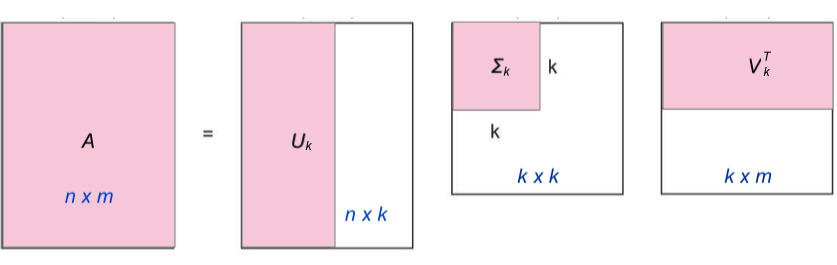
事实上隐向量矩阵可以看作是对用户和物品向量化的编码,即挖掘用户和物品在多个维度下的隐藏特征。
ALS (2008)
Alternating Least Squares(ALS): 交替最小二乘
矩阵分解求解的一种优化算法,而FunkSVD看作是基于随机梯度下降的求解
FunkSVD
既然矩阵分解的目的可以看作是得到隐向量的过程,则可以把矩阵分解转化为一个优化问题,直接初始化该隐向量,并通过迭代优化寻找满足得分矩阵的最优的隐向量。
根据R矩阵中已知的得分,计算损失:
正则化:
梯度下降:
PMF(2008)
Salakhutdinov et al. Probabilistic matrix factorization. NIPS(2008): 1257-1264.
FunkSVD的概率解释版本
BiasSVD(2009)
Koren et al. Matrix factorization techniques for recommender systems.Computer 42.8 (2009).
- $\mu$: 整体平均评分,已知常量
- $b_\mu$: 用户评分偏差, 待训练向量,与用户数目等长
- $b_i$: item被评分偏差,待训练向量,与物品数目等长
- $\hat{r}{ij}=\sum+\mu+b_u+b_i$}^{K} p_{i k} q_{k j
梯度下降:
SVD++
在BiasSVD的基础上引入隐式反馈
- $||R_u||$: $R_u$为user 打分的item的id, 因此这个值可以看作是user打分的item的个数
- $y$: (item_size, dim), 每一个item对应的权重系数矩阵
梯度下降:
timeSVD
ConvMF(2016)
- paper: Convolutional Matrix Factorization for Document Context-Aware Recommendation
- ConvMF-github
NMF
Learning the parts of objects by non-negative matrix factorization, 1999
ref
- blog:
- paper
- personal code