轨迹优化之
- elastic band
- chomp
- stomp
- trajopt
- itomp
轨迹优化的层次:安全, 轨迹平滑, 控制可行。运动规划侧重前两个, 最优控制侧重后两个。而在轨迹规划既涉及到运动规划,又涉及到最优控制,因此概念上覆盖全部的三个层次。
- collision-free:
- kinematically feasible
- dynamically feasible
优化的方法:区别在与对约束函数或者是目标函数的整理。类似于直接计算并不太好计算,而是进一步整理成另一种更加容易计算或者是更加高效的形式
2021 - Integrating Fast Regional Optimization into Sampling-based Kinodynamic Planning for Multirotor Flight
intro
- use kinodynamic rrt* as the heuristic plan, then optimized by a regional trajectory optimizer
- this optimizer is a sequence of QP problem
- regional trajectory optimizer reference:
related workd
regional optimization: consider the local domain information, such as CHOMP
problem: inefficient for narrow passage situation
methodogy
k-rrt*:
- solve BVP by Pontryagin Maximum Principle, obtaining the optimal transition time τ∗ and deriving the unconstrained optimal transition rajectory as a 5th-degree polynomial.
- check collision, if the path is violated, then relax τ to get a new polynominal
quadratic objective function:
- smoothness cost: squared jerk
- resemblance cost: distance to original trajectory
- collision cost: distance to some anchor point, which providing dragging force to draw the collided part to nearby collision-free areaas
iteractive optimization process
- solve the quadratic objective iteractively
- it cillides with new obstacles, adding new attracting points to provide accurate dragging force
- if the state and control violate saturations, increase time duration
- selection of the attracting points: 标记轨迹中碰撞区域(更高维度中很难决定哪些区域是碰撞的)的起点和终点,通过A 快速找到一条无碰撞路径。选取碰撞轨迹区段中点与A路径中点向外延伸作为
attracting point.,通过局部选择牵引点的方式避免计算碰撞梯度
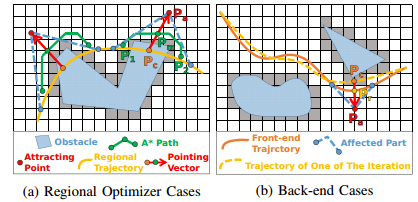
overview
对于障碍物的表达: 使用A* 选取牵引点,以与牵引点的距离作为优化梯度避开障碍物
trajectory refinement
trajopt
introduction
- use l1 penalties for equality and inequality
- computed signed distance using convex-convex collision detection
related work
轨迹优化是最优控制中的一个基本概念。
- potential field
- CHOMP
- STOMP
- ITOMP
Sequential Convex Optimization
solves a non-convex optimization problem by repeatedly constructing a convex subproblem—an approximation to the problem around the current iterate x
turning the infeasible constraints into penalty:
two loops:
- outer loop(PenaltyIteration): increase the penalty coefficient µ until all the constraints are satisfied
- next loop(ConvexifyIteration): repeatedly construct a convex approximation to the problem
l2 VS l1:
stomp
moveit 三种轨迹优化方法对比
- Time-optimal Trajectory Parameterization
- Iterative Spline Parameterization
- Iterative Parabolic Time Parameterization
time optimal path
2014-TOPP
A General, Fast, and Robust Implementation of the Time-Optimal Path Parameterization Algorithm
introduction
three families of methods:
- dynamic programming: divide the$(s, \dot{s})$ plane into a grid and find the optimal trajectory in the $(s,\dot{s})$ plane
- convex optimization: discretize the s-axis into N segments and subsequently convert into a convex optimization problem
- numerical integration: Pontryagin Maximum Principle(庞特里雅金极大原理 ), the optimal trajectory in the $(s, \dot{s})$ plane is known to be “bang-bang” and can thus be found by integrating successively the maximum and minimum accelerations $\ddot{s}$. But the programming is difficult with the so-called dynamic singularities
This paper develops a numerical integration method considering the dynamic singularities.
bang-bang control: 起停式控制,有迟滞区间。在最优控制中,若最优控制信号为其上限或下限,则该最优控制问题可以以起停式控制为最优解。起停式控制常出现在最短时间的最佳控制问题中[2]。例如要车辆行驶一定距离,且从出发到最后停止的时间要最短,其解法是在经过某一“切换点”前用最大油门加速,过切换点后以最大刹车方式刹车,让车停在想要的位置。---- wiki
improve the robustness of the numerical integration approach
General formulation of the TOPP problem:
ref
- blog
-
paper
- trajectory planning for automatic machines and robots
-
time optimal path
- Numerical Integration
- 2016-Essential Properties of Numerical Integration for Time-optimal Trajectory Planning Along a Specified Path
- 2013-A general, fast, and robust implementation of the time-optimal path parameterization algorithm
- 2018_TOPP_A New Approach to Time-Optimal Path Parameterization Based on Reachability Analysis
- 2019-Time-optimal path tracking for robots a numerical integration-like approach combined with an iterative learning algorithm
- convex optimization
- Time-Optimal Path Tracking for Robots: A Convex Optimization Approach
- 2012_IJRR_Collisionfree and smooth trajectory computation in cluttered environments
- 2012-rss-TOTG-Time-optimal trajectory generation for path following with bounded acceleration and velocity
- 2013-Fast Interpolation and Time-Optimization on Implicit Contact Submanifolds
- Numerical Integration
-
motion planning
-
2009-CHOMP:Gradient optimization techniques for efficient motion planning
- 2017_ISRR_Fast any time motion planning in point clouds by interleaving sampling and interior point optimization
- trajopt
- 2011-Parallel Algorithms for Real-time Motion Planning
- itomp
- gpmp2: Gaussian Process Motion Planner 2
- 2017 Search-based Motion Planning for Quadrotors using Linear Quadratic Minimum Time Control
-
-
grasp motion planning
- project
- Time-Optimal Path Following with Bounded Acceleration and Velocity