04_velocity
YeeKal
•
•
"#"
skew symmetric matrix
cross product
denote $a,b\in \mathcal{R}^3$,
$\hat{a}\in \mathcal{R}^{3\times 3}$: the skew-symmetric matrix.
property
angular velocity and differential of rotation matrix
对旋转矩阵求导是指旋转矩阵对时间的微分,结果是一个矩阵。而角速度是关于某一个轴的旋转速度。多个轴的角速度组合成向量的形式又称为角速度矢量。
指数积公式(轴角坐标)中旋转矩阵表示为绕一个轴旋转一定角度实现:$R=e^{\hat{w}\theta}$,则绕该轴的角速度为:$\dot{\theta}$,而微分矩阵(Caution:下式中的$\hat{w}$与上式中的不同,上式中只是表示它是一个反对称矩阵):
若把该角速度向x-y-z轴投影可得到x-y-z轴的角速度矢量:
机器人雅可比矩阵左侧的状态速度量中的姿态速度量就是指的分别绕x-y-z轴的角速度矢量。与欧拉角不同,角速度矢量中的轴没有顺序之分,是角速度向三个轴的的投影。
angular velocity vector and differential of eular angles
但是在根据旋转矩阵求欧拉角时,角度是有时序的。这样通过欧拉角表示的两矩阵之间的误差量就不能代表矩阵关于固定坐标系x-y-z的微分量,故存在一个矩阵把欧拉角坐标系速度矢量转化到角速度矢量。
- 观察投影法
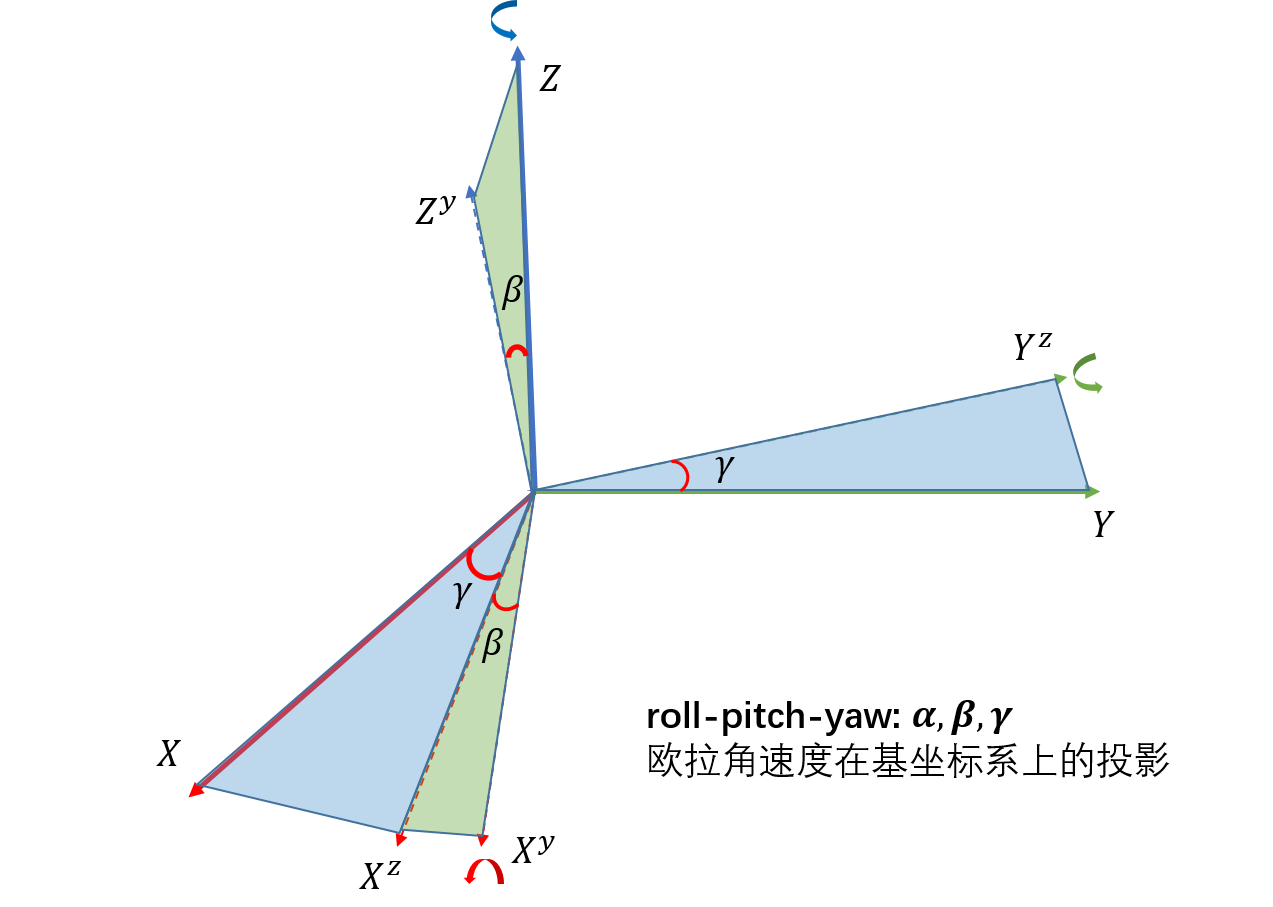
依次转动$\gamma, \beta,\alpha$,观察其转动轴在基坐标轴上的投影.其中$E_{rpy}$中第一列表示$\dot{\alpha}$转动轴分别在x-y-z上投影,第二列表示$\dot{\beta}$转动轴分别在x-y-z上投影,第三列表示$\dot{\gamma}$转动轴分别在x-y-z上投影.
- 方法二:
把转动轴变换到基坐标系: