06_dynamics
acceleration
线加速度
动点在相对坐标系B中的运动,变换到坐标系A中的表达式:
其中叉积的性质:
in revolute joint:
in prismatic joint:
角加速度
rigid body dynamics
linear momentum
angular momentum(角动量/动量矩)
(moments, 力矩)
刚体定轴转动:
so:
($I$, inertia tensor)
Newton equation and Euler equation
(此处请注意对角动量的求导,对惯性张量I的求导)
inertia tensor
parallel axis theorem
$p_C$为坐标系C原点在坐标系A中的坐标。
Newton-Euler algorithm
where the origin of frame{$C_i$} is at the center of the body, with the same orientation as frame{i}.
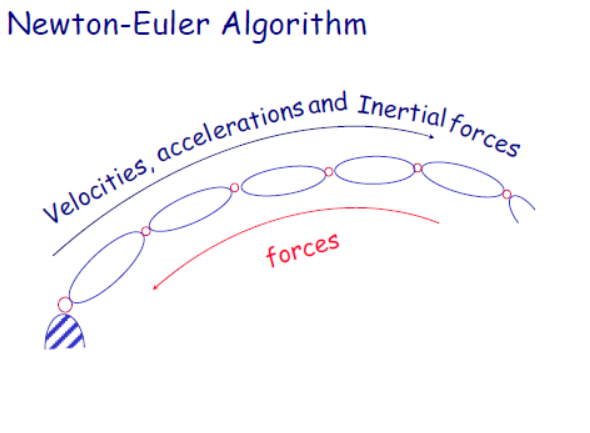
由关节位置,速度和加速度计算所需的关节力矩。
forward equation: vel, acceleration
forward:
backward
惯性张量:
设 $w=[w_x, w_y, w_z]^T$,角动量:$L=Iw$
- inverse dynamics: q to torque
- forward dynamics: torque to q
动力学方程的结构
state space equation
configuration space equation
Lagrange equation
(kinetic energy-potential energy)
kinetic energy: $K=\sum_iK_i=\sum_i(\frac{1}{2}m_i\upsilon^T_{C_i}\upsilon_{C_i}+\frac{1}{2}{}^i\omega^T_i {}^{C_i}I_i\omega_i )=\frac{1}{2}\dot{q}^TM(q)\dot{q}$
kinetic energy: work done by external forces to bring the system from rest to its current state.
two link arm
another version:
where